Move Fast

선형 변환 측면에서의 SVD

1. m x n 차원의 행렬의 의미: n차원 공간에서 m차원 공간으로 선형 변환

2. 선형 변환: 벡터 공간에서 벡터 공간으로 가는 함수로, 그것들 중 벡터 공간의 성질을 보존하는, 즉 선형성을 갖는 함수

3. 임의의 벡터 x에 행렬 A를 곱하면 벡터 x는 A에 의해 변환된 새로운 벡터 Ax가 된다.

4. 좌표 공간에서 선형 변환으로 봤을 때(기하학적 의미) 직교 행렬 (AA^T = A^TA = I, A^T = A^-1)은 회전 변환 또는 반전된 회전 변환이고, 대각 행렬(대각 원소를 제외한 모든 원소는 0)은 좌표값의 스케일 변환이다.

5. Ax = y 라고 할 때, x 의 값이 바뀔 때 만들어지는 모양(1)은 y 의 값이 바뀔 때 만들어지는 모양(2)과 약간 차이가 있다. 아래의 그림만 봤을 때는 (1)을 회전시킨 다음 길이에 변화를 주어 (2)가 된 느낌이다. 벡터의 길이가 바뀐 값들을 scaling factor라고 하며, 특이값(singular value)라고도 한다.

6. 4번에서 설명했듯이 직교 행렬은 회전 변환, 대각 행렬은 좌표값의 스케일 변환이므로 모양 (2)는 어떤 직교 행렬에 의해 회전되고나서 특이값을 대각원소로 가지는 대각 행렬에 의해 스케일 변환된 형태라고 설명할 수 있다.

7. 실제로 행렬 A는 특이값을 대각 원소로 하는 대각 행렬(Σ)과 2개의 직교 행렬 U와 V로 분해할 수 있으며, 이 방법을 특이값 분해(SVD)라고 한다. 특이값 분해의 정의는 다음과 같다.

   • A = UΣV^T

   • A : m×n rectangular matrix

   • U : m×m orthogonal matrix

   • Σ : m×n diagonal matrix

   • V : n×n orthogonal matrix

8. 정리하자면, 벡터 x를 행렬 A로 변환했을 때, Ax는 x를 먼저 V^T에 의해 회전시킨 후 Σ로 스케일을 변화시키고 다시 U로 회전시키는 것임을 알 수 있다.

   • 다시 언급하자면, 도형의 모양을 바꾸는 것은 오로지 특이값에 의해서만 결정이 된다.

특이값 분해의 증명: A = UΣV^T

먼저 두 개의 직교하는 벡터 x, y를 행렬 A에 의해 선형 변환된 결과 Ax 와 Ay 를 살펴보면, 변환 후에도 Ax와 Ay가 직교 벡터가 되는 경우가 한 번이 아님을 알 수 있다.

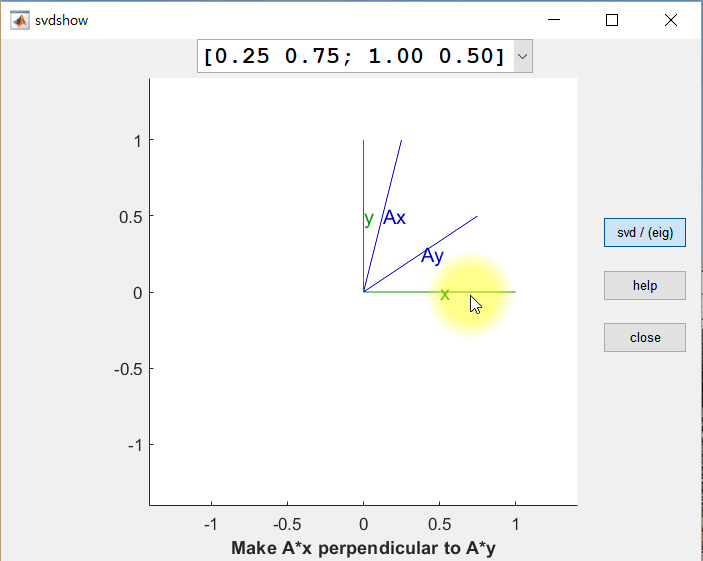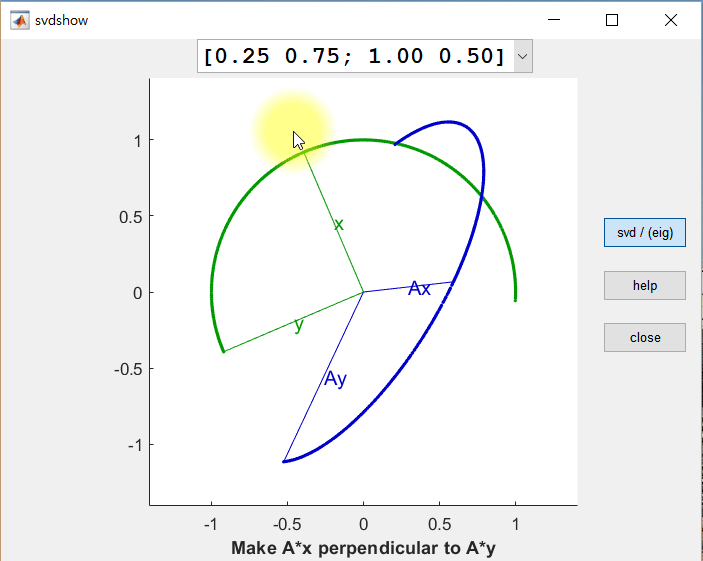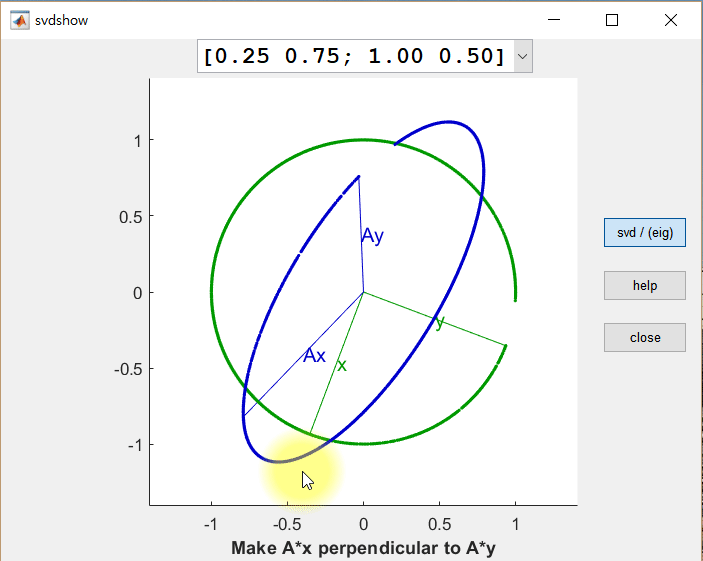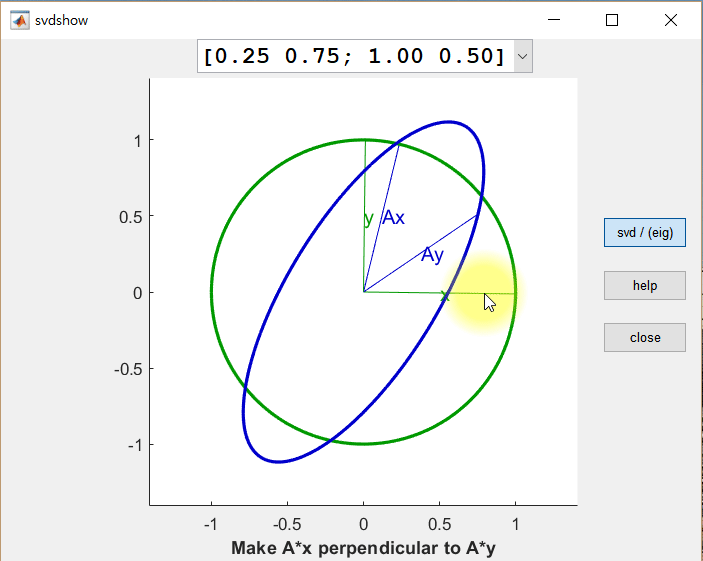
직교 벡터 x와 y를 row vector로 가지는 행렬을 V라고 했을 때, U는 선형 변환 후(Ax와 Ay) 각각의 크기를 1로 정규화한 벡터를 column vector로 가지는 행렬, Σ는 특이값들을 대각원소로 가지는 행렬로 설명할 수 있다.

즉, AV = UΣ 임을 알 수 있다. 양 옆에 V^T를 곱해주면

VV^T = I 이기 때문에 AVV^T = UΣV^T 에서 A = UΣV^T 가 된다.

특이값 분해의 활용

행렬 A에 의해 임의의 벡터를 변환한 결과를 통해 형태적인 측면에서의 변화는 오로지 특이값에 의해 결정된다는 사실을 확인했다. 임의의 벡터 뿐만 아니라 임의의 행렬도 마찬가지로 행렬 A의 대각 행렬에 의해서 변환 후 모양이 바뀐다. 즉, 특이값이 행렬의 원소를 결정짓는다는 의미이다.

그리고 행렬의 원소를 결정짓는 것은 SVD를 이용하면 행렬 A에도 적용이 가능하다. 간단하게 생각해보면 항등 행렬 I를 A로 선형 변환 시킬 때 특이값을 조정할 수 있다면 변형된 A을 얻게 될 것이다. 이는 바로 A를 곱한다는 의미가 아니라 SVD 후에 차례대로 3개의 행렬을 곱하는 경우를 의미한다. 그러나 더 쉽게 변형된 A를 얻을 수 있다. 바로 SVD로 행렬 A를 분해한 뒤 대각 행렬의 원소만 바꾸고 다시 3개의 행렬을 곱하면 된다.

예를 들어, SVD를 적용한 후에 대각 행렬에서 가장 작은 특이값 하나를 0으로 만들어서 행렬 A'을 얻었다. 이 때 A'은 원본 행렬 A와 매우 유사한데 그 이유는 가장 작은 특이값 하나만 0으로 만들었기 때문이다. 가장 작은 특이값이 의미하는 바는 행렬 A가 어떤 정보를 가지고 있느냐에 따라 다르며, 필요없는 정보를 지우고 싶다면 예시와 같이 연산을 수행할 수 있을 것이다.

예시에 대해 구체적인 상황을 덧붙이자면, 어떤 원본 데이터에 대한 행렬 A가 각 사용자가 영화에 등급을 매긴 경우라 할 때(row는 사용자, column은 영화) 이를 분해해서 얻은 U는 사용자가 각 영화의 컨셉과 얼마나 관련이 있는지를 나타내고, V^T는 각 영화의 컨셉과 해당 영화가 얼마나 관련이 있는지를 나타낸다. 그리고 Σ의 대각원소는 현재 원본 행렬에서 영화의 컨셉이 얼마나 많은 비율을 차지하는지 (높은 강도로 점유하는지)를 나타내게 된다.

여기서 가장 낮은 강도로 점유하는 특이값을 지워버리면, 실제 데이터에서 비율이 낮은 컨셉의 영화에 대한 데이터는 지워진다.

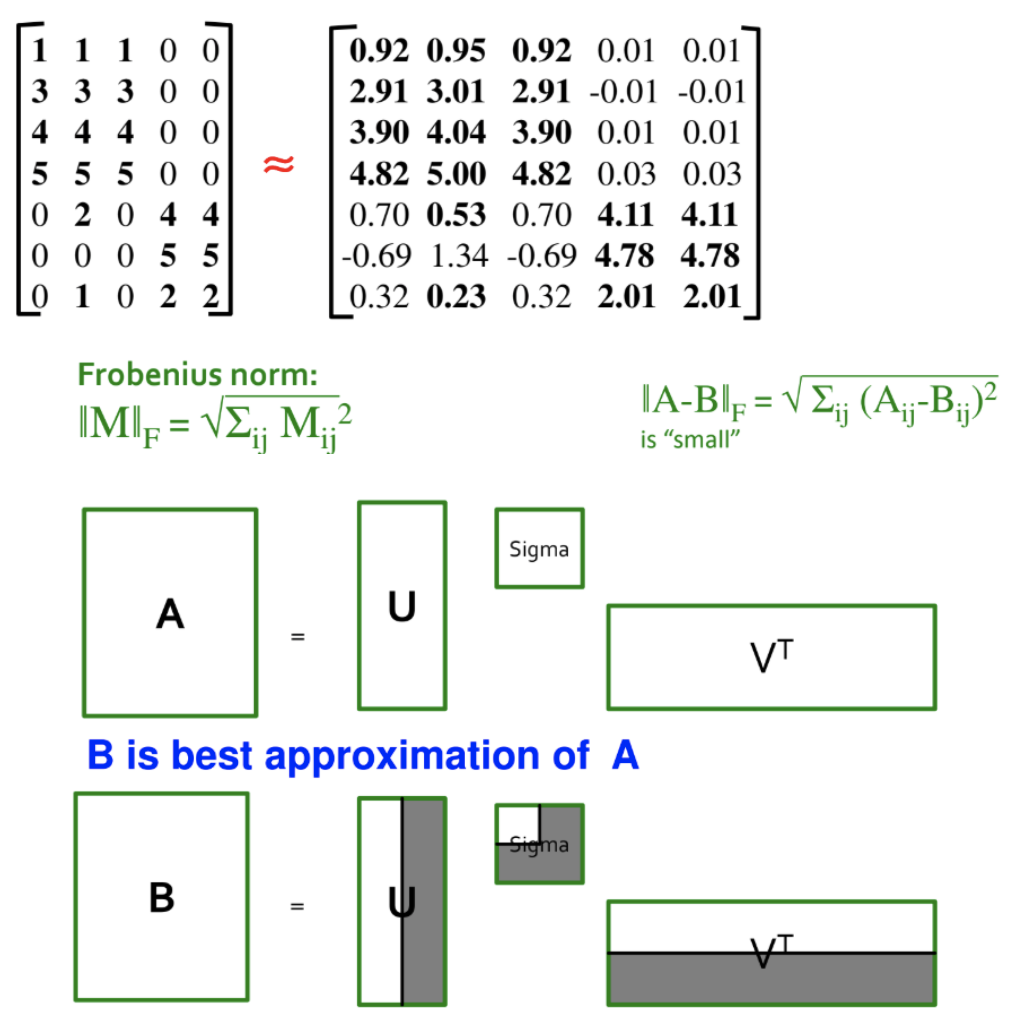
결국, 가장 작은 특이값을 0으로 만든다는 것은 원본 행렬 A에 가장 근사하면서도 불필요한 특징(noisy feature)을 제거한 행렬 B를 얻을 수 있다는 의미이며 동시에 두 개의 직교 행렬의 벡터들을 사용하지 않으니 차원을 축소했다고도 볼 수 있다.

또 다른 예시로는 이미지 압축 또는 이미지 부분 복원이 있다. 어떤 사진에 대해 픽셀값을 원소로 가지는 행렬로 표현한다면 특이값을 조정해서 사진의 본질적인 특징들을 살리고 불필요한 부분들을 없애거나 원하는 특징들만 남겨서 유용한 정보를 얻을 수 있을 것이다.

주로 차원을 축소하는 이유는 다음과 같다.

• 숨겨진 상관 관계(correlation)이나 주제를 찾기 위함
  예) Text: 공통적으로 같이 쓰이는 단어들이 있다.

• 중복되거나 쓸모없는(noisy) 특징(feature)들을 제거하기 위함

  예) Text: 모든 단어들이 유용하진 않다.

• 해석(Interpretation)과 시각화(Visualization)에 용이

• 데이터를 처리하고 저장하는게 쉽다.

참고 자료

• angeloyeo.github.io/2019/08/01/SVD.html

• darkpgmr.tistory.com/106

분류(Classification)

• 불연속적인 값(이산형 데이터 또는 범주형 데이터)을 가진 결과를 예측하는 것

• 이진 분류(binary-class classification): 데이터의 결과가 0과 1로만 표현이 되는 것

  • y∈{0,1}

  • 예를 들면, 종양 크기에 따른 악성과 양성의 유무가 있다. 악성이면 1, 양성이면 0으로 클래스를 지정할 수 있다. 여기서 종양의 크기는 독립 변수이다.

• 다중 분류(mutli-class classification): 데이터의 결과가 3개 이상으로 표현이 되는 것

  • y∈{1,2,...,N}

  • 예를 들면, 환자의 증상이 나타나는 부위와 통증의 정도에 따른 N가지 질병으로 분류하는 것이 있다. 클래스가 N가지 있고, 증상 부위 및 통증의 정도는 입력으로 들어오는 독립 변수이다.

이진 분류(Binary-class Classification)

• 이진 분류는 비용 함수를 계산하기 위해 시그모이드 함수를 이용해서 가설 함수를 바꿔준다.

• 위와 같은 함수를 로지스틱 함수(logistic function)라고 하며 이진 분류를 로지스틱 회귀(logistic regression)라고도 부른다.

• 시그모이드 함수를 사용하는 이유

  • 가설 함수의 예측값은 항상 0 ~ 1 사이의 값이어야 한다.

  • 가설 함수는 입력값 x에 대해 y = 1 일 확률을 의미해야 한다. (여기서 y는 이진 분류의 클래스 0 또는 1 이다.)

  • 클래스는 두 가지 밖에 없기 때문에 y = 1일 확률을 알면 y = 0인 확률을 알 수 있다. 두 확률의 합은 1이다.

  • 그래프를 보면 알 수 있듯이, 시그모이드 함수의 특징은 입력값(=z) >= 0 인 경우 0.5 이상의 값을 반환하고 입력값(=z) < 0 인 경우 0.5 미만의 값을 반환한다. 반대로 말하자면, h = g(z) 이므로 가설 함수의 결과(=h) >= 0.5 이면 y = 1로, 가설 함수의 결과(=h) < 0.5 이면 y = 0으로 분류할 수 있다.

  • 즉, 확률을 이용해서 데이터를 두 클래스로 분류할 수 있다.

• 단, 가설 함수의 결과가 0또는 1일 때는 무한대 값을 가진다.

• z는 선형 함수인데 (z 는 원래 가설 함수로 y = ax + b 형태) 그래프 상에서 데이터를 두 개의 클래스로 나누는 역할을 한다. 실제로 그래프에서 z > 0 인 부분은 y = 1 로 분류하고 z < 0 인 부분은 y = 0으로 분류를 한다. 이렇게 z로 데이터들을 두 클래스로 나누면 그래프에서 경계가 생기는데 이를 결정 경계(decision boundary)라고 한다.

  • 2차원 그래프의 경우 직선이나 곡선, 3차원 그래프의 경우 평면이 된다. 시그모이드 함수를 사용해서 데이터들을 분류할 때 아래 예시와 유사하게 비선형(곡선)으로 분류할 수 있게 된다. 즉, 비선형 함수로 분류하면 비선형 결저 경계(non-linear decision boundary)가 형성되고, 다항 함수에 항을 추가해서 더 복잡한 결정 경계를 만들 수도 있다. (항이 많아질수록 함수가 복잡할수록 결정 경계는 세밀해지고 복잡해진다.)

  • 결정 경계는 훈련 데이터보다는 매개변수와 관련된 가설 함수의 속성이라고 볼 수 있다.

• 로지스틱 회귀의 가설 함수는 다변량(mutlivariate)의 경우 행렬로 다음과 같이 표현될 수 있다.

• 예시: 아래와 같은 파라미터를 가지게 되면 결정 경계는 x축에 수직인 직선이 된다. x <= 5 인 데이터들은 y = 1 로 분류가 되고, x > 5인 데이터들은 y = 0으로 분류가 된다.

• 선형 회귀의 비용 함수를 그대로 사용할 경우 비용 함수의 그래프가 아래와 같이 비블록 함수의 모양을 띄게 된다. 따라서 극소점으로 착각할 수 있는 위치가 많아지게 되어 경사 하강법을 적용할 수 없게 된다.

• 로지스틱 회귀에서 비용 함수는 가설함수에 로그(log)를 씌워서 y = 1일 때와 y = 0일 때의 출력을 다르게 낸다.

  • 변경된 비용 함수는 각각 그래프가 다르지만 하나로 합치면 극소점이 하나 존재하여 경사 하강법을 적용할 수 있게 된다.

• 위와 같은 비용 함수를 편의상 한 번에 표현할 수 있는 식이 있는데, 이를 Binary Cross-Entropy 라고 한다.

  • Binary Cross-Entropy는 실제로 최대 우도 추정의 원리로 유도된 함수인데, 서로 다른 모델에 대한 매개변수를 효율적으로 찾는 방법에 대한 통계에서 나온 아이디어이다. 이에 대한 자세한 증명 과정은 여기를 참고.

• 비용 함수의 경사 하강법

• 위 식의 자세한 증명 과정은 수식으로 대체한다. 시그모이드 함수를 직접 미분해보면 알 수 있다.

다중 분류(Mutli-class Classification)

• 다중 분류는 이산형 데이터에 대해 클래스가 셋 이상일 때 적용하는 기법이다.

• One-vs-all 방식이 있는데, 각 클래스에 대해 이진 분류를 수행하는 방법이다. 예를 들어, 클래스 A, B, C가 있을 때 클래스 A에 대해 이진 분류를 하게 되면 클래스 A이면 y = 1로 분류되고, 그 외에는 y = 0으로 분류하는 것이다. 클래스 B나 C의 경우도 마찬가지로 해당 클래스일 때는 y = 1로 분류하고, 아닌 경우는 y = 0으로 분류한다.

  • 그러면 각 데이터마다 각각의 클래스에 대한 확률이 나오게 되고, 이 확률들의 합은 1이 된다. 즉, 모든 클래스의 확률의 합은 1인 것이다. 여기서 확률이 가장 높은 클래스가 해당 데이터가 분류된 클래스인 것이다.

정규화(Regularization)

• 학습할 때 사용한 데이터 외에 새로운 데이터에 대해 학습 결과가 좋지 않은 것을 과적합(Overfitting)이라고 한다. 과적합은 주로 매개변수에 비해 데이터셋이 작은 경우 발생하기 쉬운데, 그 이유는 매개변수가 많다는 것은 가설 함수가 복잡하고 곡선이 많아 데이터셋에 딱 맞는 함수를 찾을 수 밖에 없기 때문이다.

• 과적합을 피하기 위해 비용 함수의 매개변수에 제약을 거는 방법을 정규화라고 한다. 제약을 건다는 의미는 매개변수의 변화량을 제어한다는 것이다.

  • 예를 들어, 아래와 같은 가설 함수와 비용 함수가 있을 때, 경사 하강법을 적용하면 𝝷3과 𝝷4는 작은 값만 가져도 비용 함수에 영향을 많이주게 되므로 가장 작은 값을 가질 수 밖에 없다. 따라서 최종적으로 찾게 되는 함수는 2차 함수처럼 나오게 된다.

• 위의 예제처럼 비용 함수의 뒤에 추가되는 항을 regularization term 이라고 하며, 다음과 같이 수식으로 표현할 수 있다. 아래에서 람다(lamda) 값은 상수이며 regularization parameter 라고 한다.

• 정규화를 적용한 비용 함수에 대한 경사 하강법

  • 경사 하강법을 적용하면, 이미 변화량이 커서 극소점에 가까워진 파라미터는 변화량을 줄여서 조금씩 움직이도록 하고, 변화량이 작아서 극소점에서 멀어진 파라미터는 변화량을 늘려서 크게 움직이도록 하는 효과를 준다.

• 로지스틱 회귀에서 정규화 적용하기

• 정규화는 가설 함수를 단순화하는 것을 목적으로 하며, 과적합을 막는 방법으로는 파라미터의 개수를 줄이는 방법(feature의 개수를 줄이기)이 있다.

분류기(Classifier)

• 학습 데이터셋(Training Set)이 주어졌을 때, 데이터를 클래스(class) 별로 적절히 분류(classification)하는 것

• 분류가 잘 되는 함수를 찾으면, 이후 그 함수를 활용하거나 새로운 데이터가 추가될 경우 (또 다시?) 많은 실험을 거듭하여 함수를 갱신해준다.

• 함수를 찾는다는 것은 예를 들어 y = f(x) = ax + b 라고 했을 때 a와 b(=매개변수=Parameter)를 찾는 것을 의미한다.

• y = f(x) 에서 x는 데이터의 feature 또는 variable 이라고 표현이 되는데 대부분 데이터의 전처리(preprocessing) 과정에서 추출된다. 실세계의 데이터를 가공하지 않고 넣는 경우는 거의 없다. feature 마다 매개변수는 다르기 때문에 예시에서는 2개이지만 매개변수는 100개가 넘을 수도 있다. 참고로 b는 bias 라고 편향치를 나타내는 상수값인데 없는 경우가 많다. 아무튼 신경망은 이렇게 많은 매개변수를 찾는데 최적화되어 있다.

• 보통 학습 데이터가 주어질 때 입력으로 들어가는 값을 feature values (예: 크기, 강도, 색, 위치 등) 라고 하고, 출력으로 주어져야하는 값은 different classes (예: 종류, 글자, 단어, 이미지 등)라고 한다.

신경망의 구조

• 컴퓨터 과학에서 신경망은 레이어(Layer)와 노드(Node) 그리고 가중치(Weight)라는 것으로 설명이 되는데, 노드는 뉴런(Neuron)이라고도 불린다. 참고로 위키피디아에 따르면 인공 신경망의 구조는 실제 인간의 중추 신경계를 많이 참고하여 설계되었다고 한다.

• 레이어는 여러 노드로 이루어져 있고, 신경망은 여러 레이어로 이루어져 있다. 레이어는 배치된 위치에 따라 다음과 같이 3가지로 나뉜다.

  • 입력층(Input Layer): 데이터를 입력으로 받는 부분으로, 연산을 수행하지 않는다.

  • 은닉층(Hidden Layer): 복잡한 계산을 수행하는 부분으로, 모든 노드는 연산을 수행하는 함수이다.

  • 출력층(Output Layer): 계산 결과를 내보내는 부분으로, 마찬가지로 모든 노드는 연산을 수행한다.

• 인접한 두 레이어는 간선(edge)으로 연결되는데, 간선의 정점은 두 레이어의 각 노드이며, 같은 레이어의 노드끼리는 연결되지 않는다. 즉, 무수히 많은 간선이 존재하는 것이다. 가중치(Weight)는 간선에 부여되는 값으로 신경망에서는 정보를 기억 또는 학습하는 역할로 설명된다. 가중치는 값이 클수록 해당 입력이 중요하다는 것을 의미한다.

• 원하는 결과를 내는(정답을 잘 찾는) 가중치를 찾는 것이 이전에 설명했던 신경망을 이용해서 함수(=매개변수)를 찾는 것과 상동한다.

• 레이어끼리 연산하는 과정: 출력층을 제외한 모든 레이어는 바로 다음 레이어의 입력층에 해당되며, 그 이유는 이전 레이어의 연산 결과(노드의 값)를 가중치(간선의 값)와 곱해서 현재 노드의 출력으로 보내면 다음 레이어의 각 노드의 입력으로 들어가기 때문이다. 이 과정을 쉽고 빠르게 하기 위해 내적(Dot Product) 연산을 수행한다.

활성화 함수(Activation Function)

• 두 레이어간의 연산은 이전 레이어의 각 노드의 출력값(혹은 입력층의 노드 값)과 현재 레이어의 각 노드로 연결된 간선의 가중치를 곱해서 다음 레이어의 노드에 입력으로 내보내는 과정이다. 현재 레이어의 각 노드의 출력 결과를 구할 때 함수가 사용되는데, 그 함수를 활성화 함수(Activation Function)이라고 한다.

  • 함수가 사용되는 이유는 퍼셉트론의 개념을 알아야 한다. 퍼셉트론(Perceptron)은 초기 인공 신경망의 모델로, 다수의 입력으로부터 하나의 결과를 내보내는 알고리즘이다. 처음에는 은닉층이 1개(단층 퍼셉트론)였으나 입력의 개수가 많아짐에 따라 은닉층을 늘려서 다층 퍼셉트론(Multi-Layer Perceptron)이라고도 부른다.

  • 퍼셉트론에 대한 자세한 이론은 여기를 참고

• 활성화 함수는 단순히 임계값을 넘으면 1, 아니면 0을 출력하는 계단 함수(step function) 부터 복잡한 비선형 함수까지 종류가 다양하다. 이름의 의미는 어떤 임계값을 넘으면 활성화를 시킨다는 뜻에서 지어진거라고 한다.

• 레이어 마다 활성화 함수가 다를 수 있으나, 같은 레이어 내의 각 노드는 동일한 활성화 함수를 사용하며, 보통 은닉층에서는 비선형 함수가 많이 사용되고 출력층에서 최종 계산 결과로 class 를 분류할 때 선형 함수를 사용하기도 한다.

• 비선형 함수를 쓰는 이유는 레이어가 둘 이상일 때 선형 함수를 쓰면 단일 계층의 효과가 나기 때문이다. 즉, 선형 함수로는 은닉층을 여러개 추가하더라도 은닉층이 1개일 때 가중치의 배수인 단층 퍼셉트론과 차이가 없다.

• 활성화 함수의 종류

  • Sigmoid function: 입력값을 0과 1사이의 값으로 조정하여 반환하는 함수로, 그래프 상에서 S자 모양을 보인다. 주로 이진 분류(Binary Classification) 문제를 해결하기 위해 출력층에서 사용된다.

  • ReLU function: Rectified Linear Unit 의 약자이다. 입력값이 0보다 작을 경우 0을 반환(흔히 음수를 cutting 한다고 한다)하고 0보다 클 경우 입력값을 그대로 반환한다. 이미지 인식 분야에서 은닉층에서 많이 사용되는 함수로, 음수를 버릴 때(흔히 cutting 이라고 표현함) 사용한다.

  • Leaky ReLU function: 음수일 때 값을 버리지 않고 약간의 기울기를 곱한 결과를 반환하는 함수로, 은닉층에서 역전파 과정에서 미분할 때 기울기가 0이어서 발생하는 문제점들을 보완하기 위해 사용된다. 기본적으로 기울기가 0인 함수는 사용하지 않는 것이 좋은데 그 이유는 미분할 때 기울기가 소실되는 문제가 발생하면 학습이 제대로 이루어지지 않기 때문이다.

  • ELU function: Exponential Linear Unit 의 약자로, Leaky ReLU 와 모양이 거의 똑같은데 음수 부분이 지수 함수로 생겼다는 점이 다르다. 음수값이 커지는 부분에 영향을 덜 받도록 개선했다. 마찬가지로 ReLU 의 문제를 보완하기 위해 사용된다.

  • Tahn function: 입력값을 -1과 1사이의 값으로 조정하여 반환하는 함수로, 시그모이드 함수처럼 그래프 상에서 S자 모양을 보인다. 은닉층에서 종종 사용되는 함수로, 자연어 처리 분야에서 시그모이드 함수와 함께 주로 사용된다.

  • Maxout function: 입력으로 들어오는 값들 중 최댓값을 반환하는 함수이다. 은닉층이 둘 이상일 때 많이 사용되며, ReLU 와 Leaky ReLU 의 합친 것으로 보면 된다. 단점은 단일 뉴런에 대해 파라미터의 수가 2배로 증가한다는 것이다. 성능은 ReLU와 함께 가장 높게 나온다.

  • Softmax function: 3개 이상의 정답을 가지는 multi-class 데이터셋을 분류(=다중 분류)할 때 사용하는 함수이다. N개의 feature가 있을 때 softmax의 입력은 각 원소가 데이터값인 N차원의 벡터를 가정하며, 클래스의 개수가 K일 때 softmax의 출력값은 K차원의 벡터가 된다. 출력값의 각 원소는 주어진 입력이 각각의 클래스일 확률을 나타낸다. softmax는 각 클래스별로 이진 분류(로지스틱 회귀의 결과)한 결과를 원소로 가진다. 예를 들어, i번째 클래스에 대해 이진 분류할 때 i번째 클래스만 1이고 나머지 클래스에 대해 정답이 0인 것으로 간주하는 방식이다. 출력 벡터의 원소의 합은 1이라는 특징을 가집니다. K차원의 벡터를 출력하기 위해 입력값에 가중치를 곱할 때 K x N 차원의 가중치 행렬에 입력 벡터를 곱하게 됩니다.

손실 함수(Loss Function)

• 실측값(정답)과 예측값(출력층의 결과)의 차이를 수치화해주는 함수로, 비용 함수(cost function) 또는 목적 함수(objective function) 또는 오차 함수(error function)이라고도 한다.

  • 출력층에서 결과가 나왔다고 끝이 아니라, 손실 함수로 한 번 더 계산을 해주어야 한다.

• 함수의 결과가 큰 값일수록 오차가 큰 것이며 작은 값일수록 오차가 작은 것이다.

• 회귀(Regression)에서는 평균 제곱 오차(Mean Squared Error, MSE)가 쓰이고, 분류(Classification)에서는 크로스 엔트로피(Cross-Entropy)가 쓰인다.

  • 회귀(Regression)는 연속적인(continous) 값을 가진 결과를 예측하는 방법으로, 예를 들면 부동산 평수에 따른 집값 가격(연속된 숫자)을 예측하는 것(선형 회귀)이 있다. 만약 부동산 평수 외에 다른 변수가 추가되면 다항 회귀가 된다.

  • 분류(Classification)는 불연속적인(discrete) 값을 가진 결과를 예측하는 방법으로, 예를 들면 종양 크기에 따른 악성과 양성의 유무를 예측하는 것(이진 분류)이 있다. 만약 변수가 종양 크기말고 나이, 사는 장소, 종양의 색상(????) 등이 있으면 다중 분류가 된다.

• 손실 함수의 값을 최소화하는 매개변수(=가중치=Weight)를 찾는 것이 신경망의 학습(learning)이라고 한다.

• Mean Squared Error

• 이진 분류(Binary Classification): 예측값과 실측값은 모두 0(=false) 또는 1(=true)인 경우이다. 먼저, 가능도 함수(Likelihood)라는 것을 이해할 필요가 있는데, 이 함수는 관측 데이터에 대해 확률 분포의 파라미터가 얼마나 일관되는지를 나타낸다. 신경망에 대입시켜보면 관측 데이터는 학습 데이터(training set)이고 파라미터는 가중치(weight)가 될 것이다. 이진 분류에서는 베르누이 분포에 대한 가능도 함수를 이용해서 Binary Cross-Entropy 라는 것을 도출하는데 최종적으로 최소화해야 하는 수식은 다음과 같다. (개인적으로 링크를 꼭 읽어봐야 한다. 정리가 정말 잘되어 있다.)

  • 베르누이 분포는 확률의 곱이기 때문에 underflow(0으로 수렴하는) 문제가 발생할 수 있어서 가능도 함수에 log를 취한뒤 합한다. 가능도 함수는 일관되는 정도이므로 값을 최대화할 필요가 있는데, 이를 최대 우도 함수라고 한다. 그러나 최대 우도 함수를 비용 함수로 써버리면 반대로 최소화하는 상황이 되어버려 본래의 목적에 어긋난다. 따라서 -1을 곱하여 비용 목적의 함수로 사용한다.

  • 수식에 설명을 덧붙이자면 d는 실측값이고, y(x, w)는 예측값이다.

• 다중 분류(Multinomial Classification): 출력층에서 softmax 의 반환 결과(=입력에 대한 확률값)에 각 원소에 대한 binary cross-entropy를 모두 더한 결과를 최소화한다. 이에 대한 수식은 다음과 같다.

  • 마찬가지로 d는 실측값이고 y(x, w)는 예측값이다.

  • K는 클래스의 개수, N은 데이터의 개수이다.

• REMIND: 출력층의 활성화 함수와 비용 함수는 다른 것이며, 문제의 유형에 따라 조합되는 목록은 다음과 같다.

• 기타 손실 함수

  • Mean Absolute Error (MAE)

  • Mean Absolute Percentage Error (MAPE)

  • Mean Squared Logarithmic Error (MSLE)

  • Hinge Loss = max(0, 1 - t * f(x)), where t is the answer and f(x) is the predicted value.

  • Squared Hinge = Hinge Loss ^ 2

  • Sparse Categorical Cross Entropy

  • Kullback Leibler Divergence (KLD)

  • Poison: mean of (predictions - targets * log(predictions))

  • Cosine Proximity: the opposite (negative) of the mean cosine proximity between predictions and targets.