경사 하강법(Gradient Descent)
-
손실 함수를 최소화하는 방법은 그래프 상에서 최소인 지점을 찾는 것이다. 그래서 그래프 상에서 경사를 내려간다고 하여 경사 하강법이라는 이름이 붙었다.
-
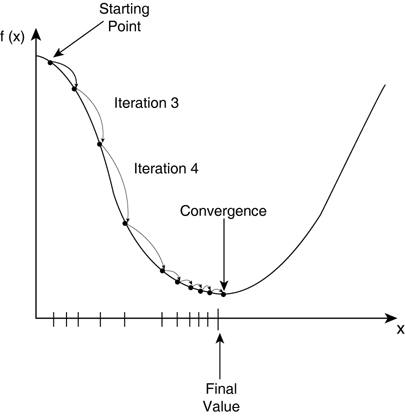
평균 제곱 오차(MSE)를 그래프에서 살펴보면, 밑으로 움푹 파인 부분이 있는데 수학에서는 극소점이라고 불리는 위치로, 극소점에 해당되는 파라미터를 찾는 것이 신경망의 목적이다.
-
결국, 신경망에서 학습이란 파라미터를 계속 움직여서(갱신해서) 극소점으로 이동시키는 과정이라고 볼 수 있다.
-
-
극소점은 함수를 파라미터에 대해 미분 했을 때 0이 나오는 파라미터를 의미(위 그래프로 따지면 x좌표)한다. 파라미터가 여러 개인 경우 각 파라미터마다 손실 함수의 미분 결과를 알아내야 한다. 여기서 미분 결과는 신경망에서는 파라미터가 손실 함수에 영향을 미치는 정도로 해석한다.
-
그래프 상에서 미분은 해당 위치의 기울기이며, 0보다 작으면 \ 모양이고, 0보다 크면 / 모양이다. 미분 값이 0보다 작으면 그래프 상에서 양수로 움직이는 방향(->)이 되고 0보다 크면 음수로 움직이는 방향(<-)이 된다.
-
즉, 미분 값의 부호와 움직이는 방향은 반대이다.
-

-
신경망에서는 경사 하강법을 적용할 때 연쇄 법칙(Chain Rule)을 활용한다.
-
먼저 연쇄 법칙이 어떤 원리로 계산되는지 살펴볼 필요가 있다.
-
어떤 두 파라미터 x, y에 대한 함수 f(x, y)가 있다고 가정하자. 각 파라미터에 대해 편미분을 하면 df / dx = y 그리고 df / dy = x 이다. 다음으로 함수 f를 파라미터로 하는 g(f(x,y)) 가 있다고 할 때, g를 x에 대해 편미분하면 dg / dx = (dg / df) * (df / dx) 이다. 만약 함수 g를 파라미터로 하는 h(g(f(x,y))) 가 있으면, h를 x와 y에 대해 각각 편미분 했을 때 도출되는 식은 다음과 같다.
-
dh / dx = (dh / dg) * (dg / dx) = (dh / dg) * (dg / df) * (df / dx)
dh / dy = (dh / dg) * (dg / dy) = (dh / dg) * (dg / df) * (df / dy)
-
h(g(f(x,y))) 같은 함수를 복합 함수(composed function)라고 하는데, 복함 함수를 미분할 때 연쇄 법칙(중첩된 함수의 미분을 연쇄적으로 곱하는 것)을 활용하면 쉽게 계산할 수 있게 된다.
-
신경망에서는 입력층을 제외한 모든 층의 각 노드는 함수의 형태(이전 레이어의 값을 입력으로 받고, 연산을 수행한 뒤 다음 레이어의 연결된 노드로 출력)이기 때문에 출력층에서 출력된 결과가 굉장히 많은 함수의 곱인 것을 알 수 있다. 실제로 노드끼리 연결된 간선은 무수히 많기 때문에 두 레이어 사이의 연산은 행렬 곱에 의해 수행되며, 결과적으로 손실 함수는 엄청나게 복잡한 복합 함수가 된다. 따라서 손실 함수를 최소화하는 파라미터를 찾기 위해 경사 하강법을 필요로 하며, 미분을 계산하는 과정에서 연쇄 법칙을 적용하는 것이다.
-
극소점이 있는 위치로 파라미터를 움직이기(갱신시키기) 위해 미분 값에 -1을 곱해서 파라미터에 더해진다. 음수를 곱하는 이유는 그래프에서 기울기의 부호와 움직여야 하는 방향이 반대이기 때문이다.

-
손실 함수(=비용 함수)를 미분한 결과에 알파(α)를 곱하는데, 이는 움직이는 간격을 조절하는 역할을 하며 학습률(learning rate)이라고 부른다. 값이 클수록 많이 움직이고, 값이 작을수록 적게 움직이기 때문에 실험을 통해 적절한 값을 찾아야 한다. 보통 0 ~ 1 사이의 값이다. 참고로 위의 수식은 모든 파라미터에 대해 적용된다.
-
참고: 경사 하강법에 대한 보다 직관적인 이해를 위해 cs231n 의 문서를 보는 것을 추천한다.
역전파법(Backpropagation)
-
입력층에서 출력층 방향으로 입력값과 가중치(=파라미터)를 곱해서 다음 층으로 전달하는 과정(즉, 손실 함수를 계산하는 과정)을 feed-forward 라고 한다. 그리고 오차를 계산하여 가중치를 갱시하는 과정을 역전파법(backpropagation)이라고 한다.
-
경사 하강법이 파라미터를 조정하는 과정은 크게 두 단계를 반복한다.
-
연쇄 법칙으로 미분을 계산한다.
-
파라미터에서 미분 * 알파를 빼서 갱신한다.
-
-
연쇄 법칙은 복잡한 함수의 미분을 쉽게 계산하게 해주지만 파라미터가 많을 수록 연산량이 많아지는 단점이 있다. 그러나 수식으로 살펴보면 다음과 같이 중복되는 연산이 많다는 것을 알 수 있다. 예를 들어, 복합 함수 h(g(f(x,y))) 를 x와 y에 대해 편미분 했을 때 아래의 밑줄 친 부분이 겹친다. 다시 말해, 파라미터가 많고, 함수가 복잡할수록 미분을 계산할 때 많은 연산이 중복된다.
dh / dx = (dh / dg) * (dg / dx) = (dh / dg) * (dg / df) * (df / dx)
dh / dy = (dh / dg) * (dg / dy) = (dh / dg) * (dg / df) * (df / dy)
-
파라미터에 z가 추가되어 똑같이 겹치는 부분이 생겼을 것이다. 따라서 실제로 구현할 때는 중복 연산을 피하기 위해 동적 계획법(Dynamic Programming)을 활용한다.
-
프로그램 관점에서 각 노드의 연산은 다음과 같이 수행된다.
-
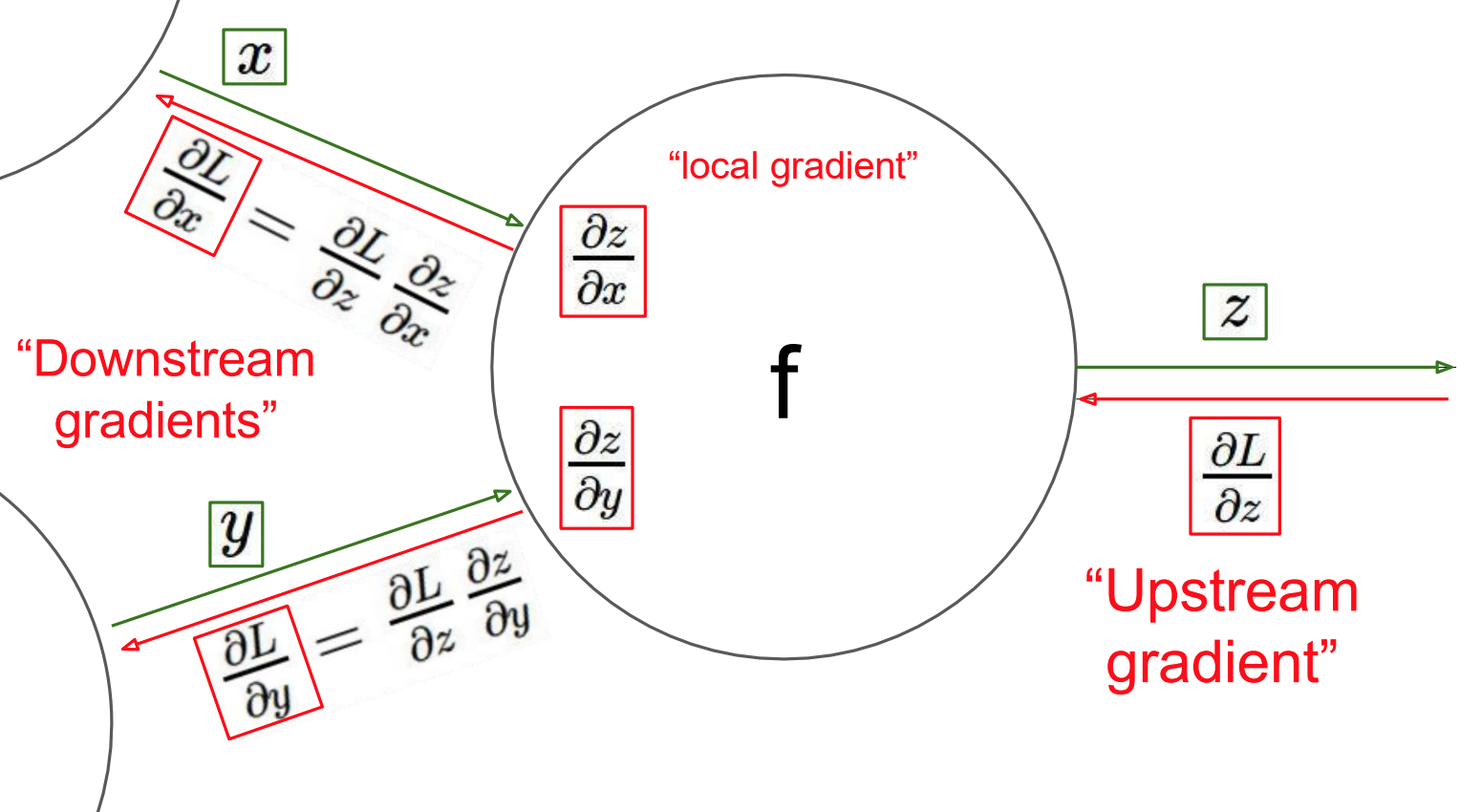
Upstream gradient: 다음 레이어의 노드에서 이미 계산된 미분으로 현재 레이어의 노드의 입력으로 들어온다.
-
Local gradient: 현재 노드의 함수를 들어오는 간선의 가중치에 대해 각각 편미분한 결과이다.
-
Downstream gradient: 위의 두 미분을 곱한 결과이며, 이전 레이어의 노드로 각 결과를 보낸다.
-
-
신경망을 큰 그림에서 살펴보면 연산이 수행되는 순서는 다음과 같을 것이다. 출력층에서 입력층 방향으로 간선들이 빛나는데 모두 각 노드의 미분(gradient)을 계산하여 이전 레이어와 연결된 간선의 가중치를 갱신하는 과정이다. 아래의 예시는 이미지 분류이다.

-
신경망에서는 위 예시처럼 현재 레이어의 노드와 연결된 다음 레이어의 노드가 하나가 아닌 여러개인 경우가 많다. 그런 경우에 upstream gradient는 모두 합해서 local gradient 와 곱한 뒤 이전 레이어로 전달된다. 더해지는 이유는 cs231n 문서를 찾아보면 알겠지만 다변수 연쇄 법칙을 따른 것이다.

-
위와 같은 신경망을 가정해보면 노드 간의 연산은 다음의 수식으로 설명된다.
-
x_k 입력값(=열 벡터)
-
W_kj 레이어 k와 i를 연결하는 간선의 가중치(=행렬)
-
net_i = W_kj * x_k (=행렬 곱)
-
f() 활성화 함수
-
O_i = f(net_i) = 레이어 j의 입력값(=열 벡터)
-
W_ij 레이어 i와 j를 연결하는 간선의 가중치(=행렬)
-
net_j = W_ij * O_i (=행렬 곱)
-
O_j = f(net_j) = 손실 함수의 입력값(=열 벡터)
-
E = loss(O_j)
-
각 결과를 미분해보면 E를 W_ki에 대해 미분한 결과를 다음과 같은 수식으로 구할 수 있다.
-


-
upstream 의 노드가 여러개인 경우는 다음과 같이 정리된다.
-
빨간색 delta_i 와 delta_j 는 캐싱되는 부분이다.
-

-
다음은 역전파법을 C++로 작성한 코드의 일부이다. 참고로 동적 계획법으로 구현하는 과정에서 캐싱되어야 하는 부분은 upstream gradient를 계산하는 부분이다. 중첩 for문에서는 upstream gradient 가 이미 계산되었다고 가정하고 현재 노드의 local gradient 를 먼저 곱한다.
void Classifier::update_weights()
{
_delta[_layer_count-1][0] = _derivative[_layer_count-1][0]; // dE/dO
for (int l=_layer_count-1; l>0; l--)
{
int order = (l == 1) ? _input_order : 0;
int node_cnt_in_curr_layer = _node_count[l];
int node_cnt_in_input_layer = _node_count[l-1];
for (int i=0; i<node_cnt_in_curr_layer; i++)
{
_delta[l][i] *= _derivative[l-1][i]; // local gradient 곱하기
for (int j=0; j<node_cnt_in_input_layer; j++)
{
// 각 입력 노드로 upstream gradient 계산해서 저장 (output node 개수만큼 더해짐)
_delta[l-1][j] += _delta[l][i] * _weight[l-1][i][j];
double delta_w = -_learning_rate * _delta[l][i] * _input[l-1][j][order];
_weight[l-1][i][j] += delta_w;
}
}
}
}
'Machine Learning > Theory' 카테고리의 다른 글
| [지도 학습 02] 로지스틱 회귀 (0) | 2021.02.09 |
|---|---|
| [지도 학습 01] 선형 회귀와 다항 회귀 (0) | 2021.02.09 |
| [심층 학습 03] 학습에 영향을 주는 요소 (0) | 2021.02.08 |
| [심층 학습 01] 신경망(Neural Network) (0) | 2021.02.07 |
| 기계 학습 개요 (0) | 2019.05.11 |