분류(Classification)
-
불연속적인 값(이산형 데이터 또는 범주형 데이터)을 가진 결과를 예측하는 것
-
이진 분류(binary-class classification): 데이터의 결과가 0과 1로만 표현이 되는 것
-
y∈{0,1}
-
예를 들면, 종양 크기에 따른 악성과 양성의 유무가 있다. 악성이면 1, 양성이면 0으로 클래스를 지정할 수 있다. 여기서 종양의 크기는 독립 변수이다.
-
-
다중 분류(mutli-class classification): 데이터의 결과가 3개 이상으로 표현이 되는 것
-
y∈{1,2,...,N}
-
예를 들면, 환자의 증상이 나타나는 부위와 통증의 정도에 따른 N가지 질병으로 분류하는 것이 있다. 클래스가 N가지 있고, 증상 부위 및 통증의 정도는 입력으로 들어오는 독립 변수이다.
-
이진 분류(Binary-class Classification)
-
이진 분류는 비용 함수를 계산하기 위해 시그모이드 함수를 이용해서 가설 함수를 바꿔준다.


-
위와 같은 함수를 로지스틱 함수(logistic function)라고 하며 이진 분류를 로지스틱 회귀(logistic regression)라고도 부른다.
-
시그모이드 함수를 사용하는 이유
-
가설 함수의 예측값은 항상 0 ~ 1 사이의 값이어야 한다.
-
가설 함수는 입력값 x에 대해 y = 1 일 확률을 의미해야 한다. (여기서 y는 이진 분류의 클래스 0 또는 1 이다.)
-
클래스는 두 가지 밖에 없기 때문에 y = 1일 확률을 알면 y = 0인 확률을 알 수 있다. 두 확률의 합은 1이다.
-
그래프를 보면 알 수 있듯이, 시그모이드 함수의 특징은 입력값(=z) >= 0 인 경우 0.5 이상의 값을 반환하고 입력값(=z) < 0 인 경우 0.5 미만의 값을 반환한다. 반대로 말하자면, h = g(z) 이므로 가설 함수의 결과(=h) >= 0.5 이면 y = 1로, 가설 함수의 결과(=h) < 0.5 이면 y = 0으로 분류할 수 있다.
-
즉, 확률을 이용해서 데이터를 두 클래스로 분류할 수 있다.
-
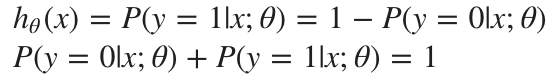


-
단, 가설 함수의 결과가 0또는 1일 때는 무한대 값을 가진다.

-
z는 선형 함수인데 (z 는 원래 가설 함수로 y = ax + b 형태) 그래프 상에서 데이터를 두 개의 클래스로 나누는 역할을 한다. 실제로 그래프에서 z > 0 인 부분은 y = 1 로 분류하고 z < 0 인 부분은 y = 0으로 분류를 한다. 이렇게 z로 데이터들을 두 클래스로 나누면 그래프에서 경계가 생기는데 이를 결정 경계(decision boundary)라고 한다.
-
2차원 그래프의 경우 직선이나 곡선, 3차원 그래프의 경우 평면이 된다. 시그모이드 함수를 사용해서 데이터들을 분류할 때 아래 예시와 유사하게 비선형(곡선)으로 분류할 수 있게 된다. 즉, 비선형 함수로 분류하면 비선형 결저 경계(non-linear decision boundary)가 형성되고, 다항 함수에 항을 추가해서 더 복잡한 결정 경계를 만들 수도 있다. (항이 많아질수록 함수가 복잡할수록 결정 경계는 세밀해지고 복잡해진다.)
-
결정 경계는 훈련 데이터보다는 매개변수와 관련된 가설 함수의 속성이라고 볼 수 있다.
-

-
로지스틱 회귀의 가설 함수는 다변량(mutlivariate)의 경우 행렬로 다음과 같이 표현될 수 있다.
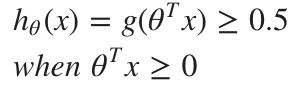

-
예시: 아래와 같은 파라미터를 가지게 되면 결정 경계는 x축에 수직인 직선이 된다. x <= 5 인 데이터들은 y = 1 로 분류가 되고, x > 5인 데이터들은 y = 0으로 분류가 된다.

-
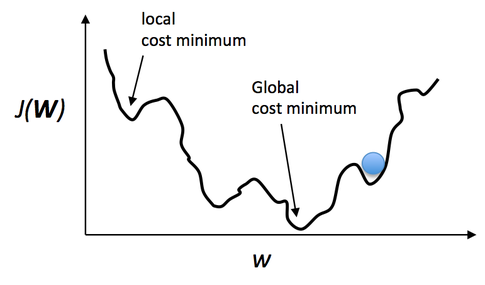
선형 회귀의 비용 함수를 그대로 사용할 경우 비용 함수의 그래프가 아래와 같이 비블록 함수의 모양을 띄게 된다. 따라서 극소점으로 착각할 수 있는 위치가 많아지게 되어 경사 하강법을 적용할 수 없게 된다.
-
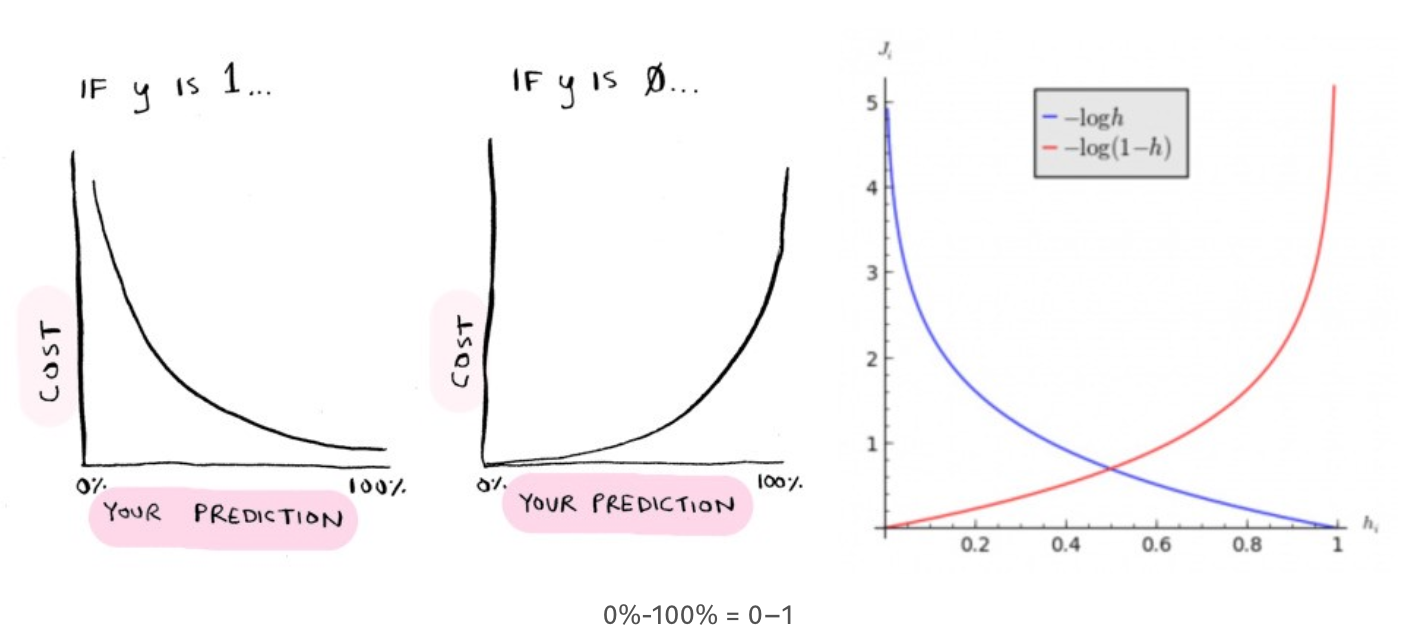
로지스틱 회귀에서 비용 함수는 가설함수에 로그(log)를 씌워서 y = 1일 때와 y = 0일 때의 출력을 다르게 낸다.
-
변경된 비용 함수는 각각 그래프가 다르지만 하나로 합치면 극소점이 하나 존재하여 경사 하강법을 적용할 수 있게 된다.
-
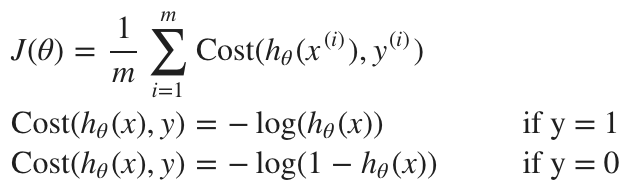
-
위와 같은 비용 함수를 편의상 한 번에 표현할 수 있는 식이 있는데, 이를 Binary Cross-Entropy 라고 한다.
-
Binary Cross-Entropy는 실제로 최대 우도 추정의 원리로 유도된 함수인데, 서로 다른 모델에 대한 매개변수를 효율적으로 찾는 방법에 대한 통계에서 나온 아이디어이다. 이에 대한 자세한 증명 과정은 여기를 참고.
-


-
비용 함수의 경사 하강법

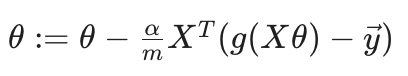
-
위 식의 자세한 증명 과정은 수식으로 대체한다. 시그모이드 함수를 직접 미분해보면 알 수 있다.



다중 분류(Mutli-class Classification)
-
다중 분류는 이산형 데이터에 대해 클래스가 셋 이상일 때 적용하는 기법이다.
-
One-vs-all 방식이 있는데, 각 클래스에 대해 이진 분류를 수행하는 방법이다. 예를 들어, 클래스 A, B, C가 있을 때 클래스 A에 대해 이진 분류를 하게 되면 클래스 A이면 y = 1로 분류되고, 그 외에는 y = 0으로 분류하는 것이다. 클래스 B나 C의 경우도 마찬가지로 해당 클래스일 때는 y = 1로 분류하고, 아닌 경우는 y = 0으로 분류한다.
-
그러면 각 데이터마다 각각의 클래스에 대한 확률이 나오게 되고, 이 확률들의 합은 1이 된다. 즉, 모든 클래스의 확률의 합은 1인 것이다. 여기서 확률이 가장 높은 클래스가 해당 데이터가 분류된 클래스인 것이다.
-

정규화(Regularization)
-
학습할 때 사용한 데이터 외에 새로운 데이터에 대해 학습 결과가 좋지 않은 것을 과적합(Overfitting)이라고 한다. 과적합은 주로 매개변수에 비해 데이터셋이 작은 경우 발생하기 쉬운데, 그 이유는 매개변수가 많다는 것은 가설 함수가 복잡하고 곡선이 많아 데이터셋에 딱 맞는 함수를 찾을 수 밖에 없기 때문이다.
-
과적합을 피하기 위해 비용 함수의 매개변수에 제약을 거는 방법을 정규화라고 한다. 제약을 건다는 의미는 매개변수의 변화량을 제어한다는 것이다.
-
예를 들어, 아래와 같은 가설 함수와 비용 함수가 있을 때, 경사 하강법을 적용하면 𝝷3과 𝝷4는 작은 값만 가져도 비용 함수에 영향을 많이주게 되므로 가장 작은 값을 가질 수 밖에 없다. 따라서 최종적으로 찾게 되는 함수는 2차 함수처럼 나오게 된다.
-


-
위의 예제처럼 비용 함수의 뒤에 추가되는 항을 regularization term 이라고 하며, 다음과 같이 수식으로 표현할 수 있다. 아래에서 람다(lamda) 값은 상수이며 regularization parameter 라고 한다.

-
정규화를 적용한 비용 함수에 대한 경사 하강법
-
경사 하강법을 적용하면, 이미 변화량이 커서 극소점에 가까워진 파라미터는 변화량을 줄여서 조금씩 움직이도록 하고, 변화량이 작아서 극소점에서 멀어진 파라미터는 변화량을 늘려서 크게 움직이도록 하는 효과를 준다.
-

-
로지스틱 회귀에서 정규화 적용하기

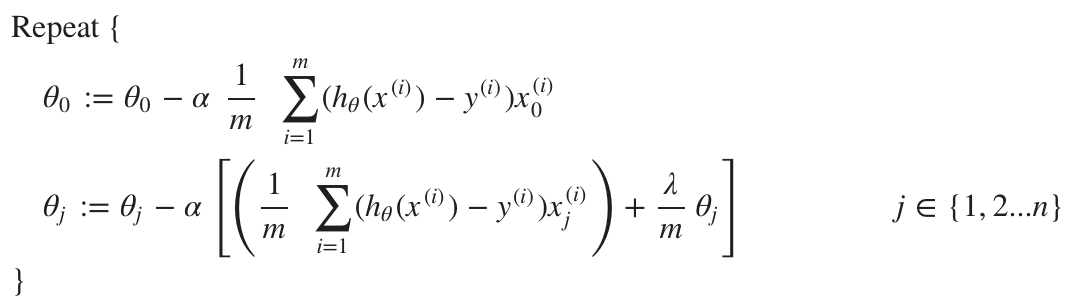
-
정규화는 가설 함수를 단순화하는 것을 목적으로 하며, 과적합을 막는 방법으로는 파라미터의 개수를 줄이는 방법(feature의 개수를 줄이기)이 있다.
'Machine Learning > Theory' 카테고리의 다른 글
| [비지도 학습 02] 차원 축소: 특이값 분해(SVD) (0) | 2021.02.13 |
|---|---|
| [비지도 학습 01] 클러스터링: K-means (0) | 2021.02.13 |
| [지도 학습 01] 선형 회귀와 다항 회귀 (0) | 2021.02.09 |
| [심층 학습 03] 학습에 영향을 주는 요소 (0) | 2021.02.08 |
| [심층 학습 02] 역전파법(Backpropagation) (0) | 2021.02.07 |