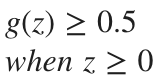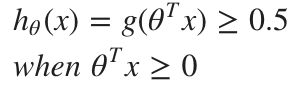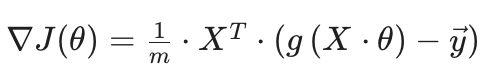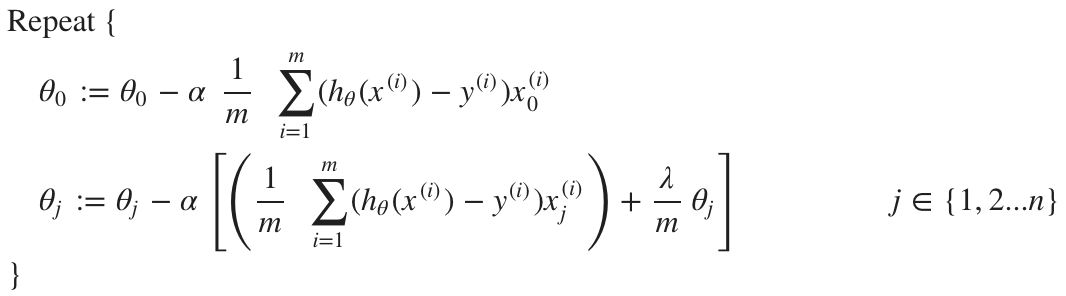Move Fast

로컬 작업 관련 명령어

• 로컬 저장소 생성: git init

• 원격 저장소 가져오기: git clone [repo_url]

• 현재 변경 사항 로컬 stage 에 올리기: git add [file_path]

  • 모든 변경사항 올리려면 파일 경로 대신 --all 옵션 사용

• stage 에 올라간 변경 사항 로컬에 반영하기: git commit -m "message"

• 원격 저장소로 변경 사항 올리기: git push [remote_repo] [branch_name]

  • 일반적으로 clone 하면 [remote_repo] 는 origin임

  • [branch_name] 은 변경 사항을 반영할 브랜치

• 현재 상태보기: git status

  • untracked file: stage에 올리지 않은 파일 목록(add 전)

• 로컬 저장소와 원격 저장소 동기화: git pull

• 로그 보기: git log

  • commit id 확인 및 HEAD 로 현재 위치한 커밋을 알 수 있음

  • 수정 전 파일과 얼마나 변경되었는지 확인하려면 --stat 옵션 사용

  • 최신순으로 k개의 파일을 보려면 -p -k 옵션 사용. k는 정수

• 이전 커밋으로 이동: git reset

  • 현재 커밋을 완전히 삭제하고 이동하려면 --hard 옵션 사용

  • 디폴트는 --mixed 이며, 커밋만 이동하고 삭제는 하지 않음. 따라서 다시 커밋을 복구할 수 있음.

  • HEAD 를 이용해서 여러 커밋을 건너뛸 수 있음.

    • HEAD^k 은 k만큼 이전 커밋으로 돌아감. k는 정수

    • HEAD~k 은 k세대만큼 이전 커밋으로 돌아감

• 현재 커밋 수정: git commit --amend

  • vim 에서 수정 후 wq로 저장하면 수정됨

• 로컬 저장소에서 문자열 탐색: git grep [keyword] [relative_path]

  • 상대 경로를 주지 않으면 현재 디렉토리부터 탐색함

브랜치 작업 관련 명령어

• 브랜치 생성: git branch [branch_name]

• 브랜치 삭제: git branch -d [branch_name]

• 브랜치 변경: git checkout [branch_name]

• 생성 후 변경: git checkout -b [branch_name]

• 브랜치 조회: git branch -v

  • 원격 저장소 브랜치와 로컬 저장소 브랜치와의 차이 확인하려면 -vv 옵션

  • 원격 브랜치는 "원격 저장소 브랜치/로컬 저장소 브랜치"로 이름이 나타남.

• 브랜치 이름 변경: git branch -m [old_name] [new_name]

• 현재 브랜치에서 분기된 브랜치를 병합: git merge [child_branch]

  • 반드시 checkout 해서 현재 브랜치에 있어야 함.

• 병합 취소: git merge --abort

• 병합한 브랜치 조회: git branch --merged

  • *는 현재 브랜치를 의미

• 병합하지 않은 브랜치 조회: git branch --no-merged

• 현재 브랜치에서 분기된 브랜치를 순서대로 커밋을 병합 (현재 브랜치에 새로운 커밋이 생성됨)

  • git rebase [base_branch] [child_branch]

  • git checkout [base_branch]

  • git merge [child_branch]

  • git branch -d [child_branch]

• 이미 push한 브랜치는 rebase로 병합하고 원격 저장소에 올릴 경우 협업중인 다른 이들이 merge해야 하는 사례가 발생할 수 있음. 따라서 push한 브랜치는 rebase로 병합하지 말 것.

• rebase 취소: git rebase --abort

• 현재 브랜치에서 분기된 둘 이상의 브랜치를 병합할 때는 rebase 를 적용하는 것이 좋음

  • merge와의 차이점은 커밋 히스토리가 선형으로 깔끔하게 남는다는 것이다.

  • 예를 들어, base_branch 브랜치에서 branch_a가 분기된 후 branch_a에서 branch_b가 분기되었을 때 branch_b에서의 변경사항만 master에 반영하고 싶다면 git rebase --onto [base_branch] [branch_a] [branch_b] 명령어를 수행

    • 이 경우 branch_a 의 변경사항은 건너뛴다는 것을 참고

  • 이후 base_branch를 최신으로 옮겨주어야 함. git checkout [base_branch] && git merge [branch_b]

  • branch_b는 이미 병합되었으므로 삭제. git branch -d [branch_b]

협업 관련 명령어

• 원격 저장소에 올라간 저장소에서 새 기능을 추가할 경우 반드시 브랜치를 생성해서 작업

  • git checkout [base_branch] && git checkout -b [new_branch]

• 원격 저장소와 로컬 저장소 동기화: git pull --rebase [remote_branch] [local_branch]

  • branch 를 별도로 주지 않으면 원격 저장소의 base_branch와 현재 branch에 대해 pull을 수행함

• merge 보다는 rebase 를 사용해서 base_branch 에 새로운 커밋을 생성해서 관리하는 것이 좋음.

  • 파생된 브랜치가 여럿이고 특정 기능에 대한 브랜치만 반영하고 싶을 때는 특히 중요.

• merge conflict 발생 시 대처법

  • 병합하기 전으로 돌리기: git merge/rebase --abort

  • git status 로 문제 파일을 찾아서 수정한 후, git merge/rebase --continue 로 계속 진행

• 이미 병합된 브랜치들을 병합 전으로 돌리기: git rebase -I HEAD^

  • HEAD 뒤에 붙는 ^의 개수는 몇 개의 브랜치까지 볼 것인지를 의미. ^^^면 3개의 브랜치를 의미

  • vim 창에서 pick -> edit 으로 수정

  • 다시 원래 브린치로 가고싶으면 git rebase --continue

• 여러 개의 커밋을 하나의 커밋으로 합치기: git rebase -i HEAD~k

  • k는 정수, 돌아갈 커밋의 개수를 의미

  • vim 창에서 pick -> f 로 수정

• 현재 브랜치 위에 특정 커밋만 가져오기: git cherry-pick [commit-id]

  • 현재 브랜치 위에 새로운 커밋이 생성됨.

  • 파일 수정 후 add한 뒤 git cherry-pick --continue

• 원격 저장소의 브랜치를 로컬 저장소에 가져오기: git checkout --track [remote_branch]

Pull Request, 원격 저장소로 PR 날리기

1. 먼저 새 저장소로 fork 후 새 저장소를 clone

2. 로컬 저장소와 원본을 연결: git remote add [repo_name] [original_repo_url]

   • repo_name 은 타이핑 편의를 위해 지어주는 닉네임을 의미

3. git remote -v

4. 새 기능 추가 시 브랜치 생성: git checkout -b [branch_name]

   • 오픈소스 컨트리뷰팅 시 "develop" 이라는 이름을 주로 사용

   • 협업 시 "feature/기능명" 이라는 이름을 주로 사용

5. 로컬 저장소에 변경사항 반영: git add --all && git commit -m "Fix <issue number>"

6. 원격 저장소에 변경사항 반영: git push origin develop

7. 깃헙 원본 저장소에서 Pull Request 클릭 후 PR 작성

8. 브랜치 병합: git checkout [base_branch] && git merge [branch_name] && git branch -d [branch_name]

9. 코드 동기화: git pull [repo_name]

선형 변환 측면에서의 SVD

1. m x n 차원의 행렬의 의미: n차원 공간에서 m차원 공간으로 선형 변환

2. 선형 변환: 벡터 공간에서 벡터 공간으로 가는 함수로, 그것들 중 벡터 공간의 성질을 보존하는, 즉 선형성을 갖는 함수

3. 임의의 벡터 x에 행렬 A를 곱하면 벡터 x는 A에 의해 변환된 새로운 벡터 Ax가 된다.

4. 좌표 공간에서 선형 변환으로 봤을 때(기하학적 의미) 직교 행렬 (AA^T = A^TA = I, A^T = A^-1)은 회전 변환 또는 반전된 회전 변환이고, 대각 행렬(대각 원소를 제외한 모든 원소는 0)은 좌표값의 스케일 변환이다.

5. Ax = y 라고 할 때, x 의 값이 바뀔 때 만들어지는 모양(1)은 y 의 값이 바뀔 때 만들어지는 모양(2)과 약간 차이가 있다. 아래의 그림만 봤을 때는 (1)을 회전시킨 다음 길이에 변화를 주어 (2)가 된 느낌이다. 벡터의 길이가 바뀐 값들을 scaling factor라고 하며, 특이값(singular value)라고도 한다.

6. 4번에서 설명했듯이 직교 행렬은 회전 변환, 대각 행렬은 좌표값의 스케일 변환이므로 모양 (2)는 어떤 직교 행렬에 의해 회전되고나서 특이값을 대각원소로 가지는 대각 행렬에 의해 스케일 변환된 형태라고 설명할 수 있다.

7. 실제로 행렬 A는 특이값을 대각 원소로 하는 대각 행렬(Σ)과 2개의 직교 행렬 U와 V로 분해할 수 있으며, 이 방법을 특이값 분해(SVD)라고 한다. 특이값 분해의 정의는 다음과 같다.

   • A = UΣV^T

   • A : m×n rectangular matrix

   • U : m×m orthogonal matrix

   • Σ : m×n diagonal matrix

   • V : n×n orthogonal matrix

8. 정리하자면, 벡터 x를 행렬 A로 변환했을 때, Ax는 x를 먼저 V^T에 의해 회전시킨 후 Σ로 스케일을 변화시키고 다시 U로 회전시키는 것임을 알 수 있다.

   • 다시 언급하자면, 도형의 모양을 바꾸는 것은 오로지 특이값에 의해서만 결정이 된다.

특이값 분해의 증명: A = UΣV^T

먼저 두 개의 직교하는 벡터 x, y를 행렬 A에 의해 선형 변환된 결과 Ax 와 Ay 를 살펴보면, 변환 후에도 Ax와 Ay가 직교 벡터가 되는 경우가 한 번이 아님을 알 수 있다.

직교 벡터 x와 y를 row vector로 가지는 행렬을 V라고 했을 때, U는 선형 변환 후(Ax와 Ay) 각각의 크기를 1로 정규화한 벡터를 column vector로 가지는 행렬, Σ는 특이값들을 대각원소로 가지는 행렬로 설명할 수 있다.

즉, AV = UΣ 임을 알 수 있다. 양 옆에 V^T를 곱해주면

VV^T = I 이기 때문에 AVV^T = UΣV^T 에서 A = UΣV^T 가 된다.

특이값 분해의 활용

행렬 A에 의해 임의의 벡터를 변환한 결과를 통해 형태적인 측면에서의 변화는 오로지 특이값에 의해 결정된다는 사실을 확인했다. 임의의 벡터 뿐만 아니라 임의의 행렬도 마찬가지로 행렬 A의 대각 행렬에 의해서 변환 후 모양이 바뀐다. 즉, 특이값이 행렬의 원소를 결정짓는다는 의미이다.

그리고 행렬의 원소를 결정짓는 것은 SVD를 이용하면 행렬 A에도 적용이 가능하다. 간단하게 생각해보면 항등 행렬 I를 A로 선형 변환 시킬 때 특이값을 조정할 수 있다면 변형된 A을 얻게 될 것이다. 이는 바로 A를 곱한다는 의미가 아니라 SVD 후에 차례대로 3개의 행렬을 곱하는 경우를 의미한다. 그러나 더 쉽게 변형된 A를 얻을 수 있다. 바로 SVD로 행렬 A를 분해한 뒤 대각 행렬의 원소만 바꾸고 다시 3개의 행렬을 곱하면 된다.

예를 들어, SVD를 적용한 후에 대각 행렬에서 가장 작은 특이값 하나를 0으로 만들어서 행렬 A'을 얻었다. 이 때 A'은 원본 행렬 A와 매우 유사한데 그 이유는 가장 작은 특이값 하나만 0으로 만들었기 때문이다. 가장 작은 특이값이 의미하는 바는 행렬 A가 어떤 정보를 가지고 있느냐에 따라 다르며, 필요없는 정보를 지우고 싶다면 예시와 같이 연산을 수행할 수 있을 것이다.

예시에 대해 구체적인 상황을 덧붙이자면, 어떤 원본 데이터에 대한 행렬 A가 각 사용자가 영화에 등급을 매긴 경우라 할 때(row는 사용자, column은 영화) 이를 분해해서 얻은 U는 사용자가 각 영화의 컨셉과 얼마나 관련이 있는지를 나타내고, V^T는 각 영화의 컨셉과 해당 영화가 얼마나 관련이 있는지를 나타낸다. 그리고 Σ의 대각원소는 현재 원본 행렬에서 영화의 컨셉이 얼마나 많은 비율을 차지하는지 (높은 강도로 점유하는지)를 나타내게 된다.

여기서 가장 낮은 강도로 점유하는 특이값을 지워버리면, 실제 데이터에서 비율이 낮은 컨셉의 영화에 대한 데이터는 지워진다.

결국, 가장 작은 특이값을 0으로 만든다는 것은 원본 행렬 A에 가장 근사하면서도 불필요한 특징(noisy feature)을 제거한 행렬 B를 얻을 수 있다는 의미이며 동시에 두 개의 직교 행렬의 벡터들을 사용하지 않으니 차원을 축소했다고도 볼 수 있다.

또 다른 예시로는 이미지 압축 또는 이미지 부분 복원이 있다. 어떤 사진에 대해 픽셀값을 원소로 가지는 행렬로 표현한다면 특이값을 조정해서 사진의 본질적인 특징들을 살리고 불필요한 부분들을 없애거나 원하는 특징들만 남겨서 유용한 정보를 얻을 수 있을 것이다.

주로 차원을 축소하는 이유는 다음과 같다.

• 숨겨진 상관 관계(correlation)이나 주제를 찾기 위함
  예) Text: 공통적으로 같이 쓰이는 단어들이 있다.

• 중복되거나 쓸모없는(noisy) 특징(feature)들을 제거하기 위함

  예) Text: 모든 단어들이 유용하진 않다.

• 해석(Interpretation)과 시각화(Visualization)에 용이

• 데이터를 처리하고 저장하는게 쉽다.

참고 자료

• angeloyeo.github.io/2019/08/01/SVD.html

• darkpgmr.tistory.com/106

클러스터링

주어진 데이터셋을 학습시켜 다른 변수들에 의해 연관성이 있거나 유사한 것들로 나누는 것

K-means

• 주어진 데이터셋을 K개의 클러스터로 나누는 방법

• 클러스터의 중심에 대한 정의

  • centroid: 데이터의 평균값을 이용

  • clustroid: 클러스터 내 점들과 가장 가까운 점(데이터셋에 있는 좌표)

• 거리에 대한 정의: 데이터간의 가까움은 유클리디안 거리로 계산되며, 코사인 유사도나 자카르드 유사도, 에딧 디스턴스 등이 있긴 하다.

• K-means 는 먼저 클러스터의 개수를 정하고 클러스터링을 수행한다.

• 알고리즘 

  1. 클러스터별 하나의 점(centroid)를 선택해서 클러스터를 초기화한다.

     • 랜덤으로 점을 고를 수도 있다. 단, K-1개의 다른 점들은 가능한 멀리 떨어져 있어야 한다.

  2. 각 점을 그 점과 가장 가까운 centroid를 갖는 클러스터에 포함시킨다.

  3. 모든 점들이 할당된 후, K개의 클러스터들의 centroid 위치를 갱신한다.

     • 현재 클러스터에 포함된 모든 점들의 평균을 계산해서 다시 구한다.

  4. 2번 과정으로 돌아가서 클러스터 내 데이터들이 바뀌지 않을 때까지 반복한다.

• K를 선택하는 방법: 엘보우 기법

  • 클러스터 개수를 늘렸을 때 centroid 간의 평균 거리가 더 이상 많이 감소하지 않는 경우의 K를 선택하는 방법.

  • 개수가 늘 때마다 평균값이 급격히 감소하는데 적절한 K가 발견되면 매우 천천히 감소한다.

  • 그래프 상에서 이 부분이 팔꿈치랑 닮아서 엘보우 기법이라고 한다.

  • 참고로, 클러스터 개수가 적으면 centroid 간의 거리가 매우 커지며, 적절한 개수이면 거리가 점점 짧아진다. 개수가 많으면 평균 거리가 매우 조금씩 줄어든다.

• K를 선택하는 방법: 실루엣 기법

  • 각 데이터의 실루엣 계수를 계산한다. 클러스터의 개수가 최적화되어 있으면 실루엣 계수는 1에 가까운 값이 된다.

  • 실루엣 계수의 평균이 0.7보다 크면 잘 분류되었다고 본다.

  • 엘보우 기법에 비해 계산하는데 시간이 굉장히 오래걸린다.

계층적 클러스터링

BFR

CURE

분류(Classification)

• 불연속적인 값(이산형 데이터 또는 범주형 데이터)을 가진 결과를 예측하는 것

• 이진 분류(binary-class classification): 데이터의 결과가 0과 1로만 표현이 되는 것

  • y∈{0,1}

  • 예를 들면, 종양 크기에 따른 악성과 양성의 유무가 있다. 악성이면 1, 양성이면 0으로 클래스를 지정할 수 있다. 여기서 종양의 크기는 독립 변수이다.

• 다중 분류(mutli-class classification): 데이터의 결과가 3개 이상으로 표현이 되는 것

  • y∈{1,2,...,N}

  • 예를 들면, 환자의 증상이 나타나는 부위와 통증의 정도에 따른 N가지 질병으로 분류하는 것이 있다. 클래스가 N가지 있고, 증상 부위 및 통증의 정도는 입력으로 들어오는 독립 변수이다.

이진 분류(Binary-class Classification)

• 이진 분류는 비용 함수를 계산하기 위해 시그모이드 함수를 이용해서 가설 함수를 바꿔준다.

• 위와 같은 함수를 로지스틱 함수(logistic function)라고 하며 이진 분류를 로지스틱 회귀(logistic regression)라고도 부른다.

• 시그모이드 함수를 사용하는 이유

  • 가설 함수의 예측값은 항상 0 ~ 1 사이의 값이어야 한다.

  • 가설 함수는 입력값 x에 대해 y = 1 일 확률을 의미해야 한다. (여기서 y는 이진 분류의 클래스 0 또는 1 이다.)

  • 클래스는 두 가지 밖에 없기 때문에 y = 1일 확률을 알면 y = 0인 확률을 알 수 있다. 두 확률의 합은 1이다.

  • 그래프를 보면 알 수 있듯이, 시그모이드 함수의 특징은 입력값(=z) >= 0 인 경우 0.5 이상의 값을 반환하고 입력값(=z) < 0 인 경우 0.5 미만의 값을 반환한다. 반대로 말하자면, h = g(z) 이므로 가설 함수의 결과(=h) >= 0.5 이면 y = 1로, 가설 함수의 결과(=h) < 0.5 이면 y = 0으로 분류할 수 있다.

  • 즉, 확률을 이용해서 데이터를 두 클래스로 분류할 수 있다.

• 단, 가설 함수의 결과가 0또는 1일 때는 무한대 값을 가진다.

• z는 선형 함수인데 (z 는 원래 가설 함수로 y = ax + b 형태) 그래프 상에서 데이터를 두 개의 클래스로 나누는 역할을 한다. 실제로 그래프에서 z > 0 인 부분은 y = 1 로 분류하고 z < 0 인 부분은 y = 0으로 분류를 한다. 이렇게 z로 데이터들을 두 클래스로 나누면 그래프에서 경계가 생기는데 이를 결정 경계(decision boundary)라고 한다.

  • 2차원 그래프의 경우 직선이나 곡선, 3차원 그래프의 경우 평면이 된다. 시그모이드 함수를 사용해서 데이터들을 분류할 때 아래 예시와 유사하게 비선형(곡선)으로 분류할 수 있게 된다. 즉, 비선형 함수로 분류하면 비선형 결저 경계(non-linear decision boundary)가 형성되고, 다항 함수에 항을 추가해서 더 복잡한 결정 경계를 만들 수도 있다. (항이 많아질수록 함수가 복잡할수록 결정 경계는 세밀해지고 복잡해진다.)

  • 결정 경계는 훈련 데이터보다는 매개변수와 관련된 가설 함수의 속성이라고 볼 수 있다.

• 로지스틱 회귀의 가설 함수는 다변량(mutlivariate)의 경우 행렬로 다음과 같이 표현될 수 있다.

• 예시: 아래와 같은 파라미터를 가지게 되면 결정 경계는 x축에 수직인 직선이 된다. x <= 5 인 데이터들은 y = 1 로 분류가 되고, x > 5인 데이터들은 y = 0으로 분류가 된다.

• 선형 회귀의 비용 함수를 그대로 사용할 경우 비용 함수의 그래프가 아래와 같이 비블록 함수의 모양을 띄게 된다. 따라서 극소점으로 착각할 수 있는 위치가 많아지게 되어 경사 하강법을 적용할 수 없게 된다.

• 로지스틱 회귀에서 비용 함수는 가설함수에 로그(log)를 씌워서 y = 1일 때와 y = 0일 때의 출력을 다르게 낸다.

  • 변경된 비용 함수는 각각 그래프가 다르지만 하나로 합치면 극소점이 하나 존재하여 경사 하강법을 적용할 수 있게 된다.

• 위와 같은 비용 함수를 편의상 한 번에 표현할 수 있는 식이 있는데, 이를 Binary Cross-Entropy 라고 한다.

  • Binary Cross-Entropy는 실제로 최대 우도 추정의 원리로 유도된 함수인데, 서로 다른 모델에 대한 매개변수를 효율적으로 찾는 방법에 대한 통계에서 나온 아이디어이다. 이에 대한 자세한 증명 과정은 여기를 참고.

• 비용 함수의 경사 하강법

• 위 식의 자세한 증명 과정은 수식으로 대체한다. 시그모이드 함수를 직접 미분해보면 알 수 있다.

다중 분류(Mutli-class Classification)

• 다중 분류는 이산형 데이터에 대해 클래스가 셋 이상일 때 적용하는 기법이다.

• One-vs-all 방식이 있는데, 각 클래스에 대해 이진 분류를 수행하는 방법이다. 예를 들어, 클래스 A, B, C가 있을 때 클래스 A에 대해 이진 분류를 하게 되면 클래스 A이면 y = 1로 분류되고, 그 외에는 y = 0으로 분류하는 것이다. 클래스 B나 C의 경우도 마찬가지로 해당 클래스일 때는 y = 1로 분류하고, 아닌 경우는 y = 0으로 분류한다.

  • 그러면 각 데이터마다 각각의 클래스에 대한 확률이 나오게 되고, 이 확률들의 합은 1이 된다. 즉, 모든 클래스의 확률의 합은 1인 것이다. 여기서 확률이 가장 높은 클래스가 해당 데이터가 분류된 클래스인 것이다.

정규화(Regularization)

• 학습할 때 사용한 데이터 외에 새로운 데이터에 대해 학습 결과가 좋지 않은 것을 과적합(Overfitting)이라고 한다. 과적합은 주로 매개변수에 비해 데이터셋이 작은 경우 발생하기 쉬운데, 그 이유는 매개변수가 많다는 것은 가설 함수가 복잡하고 곡선이 많아 데이터셋에 딱 맞는 함수를 찾을 수 밖에 없기 때문이다.

• 과적합을 피하기 위해 비용 함수의 매개변수에 제약을 거는 방법을 정규화라고 한다. 제약을 건다는 의미는 매개변수의 변화량을 제어한다는 것이다.

  • 예를 들어, 아래와 같은 가설 함수와 비용 함수가 있을 때, 경사 하강법을 적용하면 𝝷3과 𝝷4는 작은 값만 가져도 비용 함수에 영향을 많이주게 되므로 가장 작은 값을 가질 수 밖에 없다. 따라서 최종적으로 찾게 되는 함수는 2차 함수처럼 나오게 된다.

• 위의 예제처럼 비용 함수의 뒤에 추가되는 항을 regularization term 이라고 하며, 다음과 같이 수식으로 표현할 수 있다. 아래에서 람다(lamda) 값은 상수이며 regularization parameter 라고 한다.

• 정규화를 적용한 비용 함수에 대한 경사 하강법

  • 경사 하강법을 적용하면, 이미 변화량이 커서 극소점에 가까워진 파라미터는 변화량을 줄여서 조금씩 움직이도록 하고, 변화량이 작아서 극소점에서 멀어진 파라미터는 변화량을 늘려서 크게 움직이도록 하는 효과를 준다.

• 로지스틱 회귀에서 정규화 적용하기

• 정규화는 가설 함수를 단순화하는 것을 목적으로 하며, 과적합을 막는 방법으로는 파라미터의 개수를 줄이는 방법(feature의 개수를 줄이기)이 있다.