회귀 분석(Regression Analysis)
-
위키백과에 따른 정의는 다음과 같다.
-
관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법
-
회귀분석은 시간에 따라 변화하는 데이터나 어떤 영향, 가설적 실험, 인과 관계의 모델링등의 통계적 예측에 이용될 수 있다.
-
-
회귀 분석은 하나의 종속변수와 하나의 독립변수 사이의 관계를 분석하는 단순 회귀 분석과 하나의 종속변수와 여러 독립변수 사이의 관계를 분석하는 다중 회귀 분석으로 나뉜다.
-
통계학에서 독립변수(independent variable)와 종속변수(dependent variable)는 실험으로 획득한 데이터를 통해 수학적 모델을 세우거나 통계적 모델을 세울 때 사용되는 변수의 두 종류다. 종속변수가 독립변수에 의해 영향을 받는다고, 즉 종속되어있다고 해석하기 때문에 이러한 이름이 붙여졌다. 따라서 독립변수는 입력값이나 원인을 나타내며, 종속변수는 결과물이나 효과를 나타낸다. 기타 여러 가지 원인으로 관찰 중인 변수들은 기타 변수라고 한다.
-
예를 들어, y = 3x + 5 라는 함수가 있을 때 y는 x에 따라 값이 변하므로 종속변수이고, x는 독립변수이다.
-
-
정리하자면, 회귀 문제는 연속된 값을 가진 결과를 예측하는 것으로 볼 수 있고, 예측하는 함수를 찾는 것이 회귀 분석의 목적이다.
-
예를 들어, 부동산 평수에 따른 집값 가격 예측이 있다.
-
다음과 같은 좌표계에서 x축이 부동산 평수이고, 우측이 집값 가격이라고 할 때 빨간색 선형 함수는 두 변수를 잘 설명한다고 볼 수 있다.
-

-
기계 학습에서는 회귀 분석을 수행하는 모델을 회귀 모델(Regression Model)이라고 하며, 크게 선형 회귀와 다항 회귀 두 가지 방법으로 학습을 진행한다.
-
회귀 모델은 위의 두 개 말고도 다양하게 있다.
-
연속형(continous) 데이터가 아닌 범주형(categorical) 데이터에 대해서는 로지스틱 회귀(Logistic Regression)라는 예측 모델을 적용할 수 있는데 회귀 분석의 목표와는 일치하나 분류(classification) 기법의 한 종류로 본다. 이름에 회귀가 붙은 것은 역사적인 이유라고 한다.
-
-
예측의 정확도 판단
-
회귀 모델이 학습으로 찾은 함수를 가설 함수(hypothesis function)라고 하며, 예측 결과의 정확도를 판단하는 함수를 비용 함수(cost function)라고 한다.
-
회귀 모델에서 비용 함수는 평균 제곱 오차(Mean Squared Error, MSE)가 사용되며, 가설 함수의 결과(=예측값)와 실측값(=정답)의 오차 제곱의 합이 그것이다.
-
좌표계에서 평균 제곱 오차의 의미는 다음 그림으로 설명된다. 거리는 예측값과 실측값의 차이이며, 모든 데이터에 대해 이 값이 가장 작은 함수가 바로 찾고자 하는 가설 함수이다.
-

선형 회귀(Linear Regression)
-
단변량 선형 회귀(Univariate Linear Regression): 변수(variable or feature) 또는 독립변수가 1개인 데이터를 예측하는 것. 종속 변수와 독립 변수가 각각 1개씩 있어서 2차원 좌표계에 데이터를 나타낼 수 있다.
-
파라미터가 1개인 가장 단순한 가설 함수는 다음과 같다.
-

-
비용 함수는 오차제곱합으로 다음과 같이 정의된다.
-
x_i는 변수에서 i번째 값(그래프 상의 x좌표값)이고, y_i는 변수에서 i번째 실측값(label, 그래프 상의 y좌표값)이다.
-
맨 앞에 2를 나누는 것은 미분 했을 때 계산의 편의성 때문이다.
-

-
파라미터에 따른 가설함수와 비용함수 그래프는 다음과 같다.
-
비용 함수의 극소점 == 찾고자 하는 가설 함수의 파라미터
-
즉, 비용 함수 그래프 상에서 극소점으로 갈수록 가설 함수는 정답에 가까워진다.
-
이러한 이유로 비용 함수를 최소화하는 것이 회귀의 목표이다.
-

-
파라미터가 2개인 일반적인 선형 함수 형태
-
비용 함수는 두 파라미터를 입력으로 받기 때문에 3차원 그래프로 나타낼 수 있다.
-
MSE 함수의 특성상 비용 함수는 항상 극소점이 1개만 존재한다. 이러한 모양의 함수를 볼록 함수(convex function)이라고 한다.
-



-
파라미터가 2개인 비용 함수는 2차원 그래프에서 아래와 같이 등고선 형태로 표현할 수 있으며, 작은 타원에 멀리 떨어진 등고선일수록 극소점에서 멀리 떨어진 좌표이다.

-
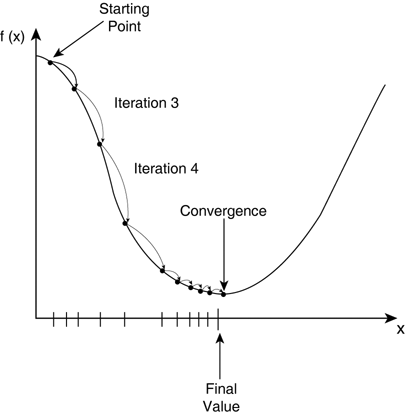
경사 하강법(gradient descent): 비용 함수의 최솟값을 구하는 알고리즘
-
비용 함수의 극소점으로 파라미터를 계속 움직이기 위해 학습률(아래 공식의 알파값)과 기울기를 곱해서 빼는 방법
-
학습률을 곱하는 이유: 학습률은 상수이며 움직이는 변화량을 조절하는 것이 목적이다. 보통 0~1 사이의 값
-
기울기를 곱하는 이유: 기울기는 극소점과 떨어진 거리와 비례하는 변화량을 갖기 때문이다. 즉, 극소점에서 멀리 있으면 비용함수의 그래프에서 해당 기울기가 가파르기 때문에 많이 움직일 수 있고, 극소점에 가까이 있으면 완만한 기울기를 가지므로 적게 움직이게 된다.
-
학습률과 기울기의 곱을 빼는 이유: 미분값의 부호는 극소점으로 이동하는 방향과 반대이기 때문이다.
-


-
실제로 각 파라미터들은 별도로 갱신되어야 하며 구현할 때 동시에 갱신되어야 한다.

-
학습률은 너무 크면 비용함수의 그래프를 벗어날 수 있고, 너무 작으면 학습 속도가 매우 느리게 되므로, 적절한 학습률을 찾는 것은 많은 실험을 필요로 한다.


-
다변량 선형 회귀(Mutlivariate Linear Regession): 변수(feature)가 2개 이상인 데이터의 결과를 예측하는 것
-
가설 함수는 다음과 같은 형태이며, n은 (feature의 개수 + 1)이다. +1은 bias 인 첫번째 파라미터를 포함한 것이다.

-
변수가 여러개이기 때문에 데이터셋을 테이블 형태로 나타냈을 때 x_i는 i번째 행의 데이터를 벡터로 나타내어 전체 데이터셋을 x_i로 구성된 행렬로 표현할 수 있다. 표기법은 다음과 같다.

-
데이터셋의 각 행을 열 벡터로 두고 파라미터 벡터와 행렬 곱 연산을 해서 가설 함수를 구할 수 있다. 아래의 수식은 입력 데이터 하나를 의미한다.

-
전체 입력 데이터는 X라는 행렬로 표현할 수 있고, X는 각 행에 입력 데이터 하나를 row vector로 포함한다.
-
전체 데이터에 대한 가설 함수는 행렬과 벡터의 곱으로 표현된다.
-


-
오차제곱합을 벡터에 대한 연산으로 표현하면 다음과 같은 수식을 얻을 수 있으며, 비용 함수를 각 파라미터에 대한 편미분으로 0이되는 파라미터 값을 모두 찾아야 한다.






-
Feature Scaling: 서로 다른 변수들은 범위가 달라서 비용함수의 그래프에서 파라미터를 임의 값으로 했을 때 극소점하고 멀리 떨어져 있을 확률이 높다. 비용 함수의 그래프가 3차원일 때 매우 넓게 퍼져 있음. 변수의 범위가 많이 차이가 날 경우 경사 하강법에 시간이 오래 걸리는 단점이 있다. 따라서, 학습 속도를 높이기 위해 변수의 범위가 모두 동일하도록 스케일링 해주어야 한다.
-
보통 모든 변수의 범위를 -1 ~ 1 사이로 스케일링함
-
단, 어떤 변수의 범위 차이가 많이 나면 안된다. -100 ~ 100 인 거랑 -0.0001 ~ 0.0001 인 경우 두 feature 에 대해 전처리를 해주어야 한다.
-
너무 정확할 필요는 없다. 경사 하강법이 빨라지기만 하면 된다.
-
We can speed up gradient descent by having each of our input values in roughly the same range. This is because θ will descend quickly on small ranges and slowly on large ranges, and so will oscillate inefficiently down to the optimum when the variables are very uneven.
-
아래는 스케일링 전후 비용 함수의 그래프 모양을 나타낸 것이다. 각 feature의 범위가 고르게 형성되면 비용 함수가 한쪽으로 치우치거나 편향된 모양이 아니게 된다.

-
Mean normalization: 각 데이터에 일반적으로 적용되는 방식으로, feature 내 평균값을 뺀 다음 feature 의 범위로 나눠준다.

-
경사 하강법 디버깅: 적절한 학습률을 찾고 싶거나, 경사 하강법이 제대로 적용되고 있는지 확인할 때 다음과 같이 반복 횟수별 비용함수의 결과를 그래프로 나타내서 디버깅을 할 수 있다. 경사 하강법이 올바르게 작동하는 경우 매 반복마다 비용 함수가 줄어드는 것이 수학적으로 증명되었기 때문에 그래프가 감소하는 형태가 아니라면 코드를 고쳐야 할 것이다.

-
학습률이 너무 작으면 천천히 수렴하고, 너무 크면 매 반복마다 비용 함수가 증가하여 수렴하지 않을 수 있다. 따라서, 아래와 같이 0.001 부터 3배씩 학습률을 늘려보면서 적절한 값을 찾을 필요가 있다. 10배씩 차이를 두기 보다 3배가 적당하다고 한다.

-
아래의 그림에서 A는 학습률이 0.1 일때, B는 학습률이 0.01 일 때, C는 학습률이 1일 때의 그래프이다. A의 그래프는 학습률이 0.1로 처음에는 크게 비용 함수가 떨어지다가 어느 정도부터 천천히 낮아지는 것을 볼 수 있다. B의 그래프는 학습률이 0.01로 처음부터 천천히 값이 떨어진다.

다항 회귀(Polynomial Regression)
-
항이 여러 개인 가설 함수로 결과를 예측하는 회귀 분석 방법이다.
-
항은 제곱근이나 2차항, 3차항 등 다양하게 있으며 함수의 형태가 비선형이라는 특징이 있다.
-
다항 회귀를 활용하는 한 가지 방법은 서로 다른 두 Feature 를 하나의 feature로 만들어서 해당 feature를 입력으로 2차 이상의 함수를 예측하는 것이다.
-
예를 들어, 부동산에서 집값 예측 시 땅의 가로/세로 길이가 주어졌을 때 면적(=가로*세로)으로 만들어서 면적에 따른 결과를 예측하기
-
새 feature 에 대해 그래프를 그렸을 때 데이터를 잘 표현하는 비선형 함수를 찾아야 한다.
-
새 feature 에 대해서도 feature scaling 을 적절히 해주어야 한다. 특히, 실수의 곱이나 범위가 큰 두 feature의 곱은 너무 0에 가깝거나 너무 큰 수가 되버릴 수 있다.
-
-
보통 2차함수는 중간에 하강하므로 3차(cubic) 함수부터 아니면 단조증가하는 제곱근이나 로그 함수를 많이 쓴다.

We can improve our features and the form of our hypothesis function in a couple different ways.
We can change the behavior or curve of our hypothesis function by making it a quadratic, cubic or square root function (or any other form).
One important thing to keep in mind is, if you choose your features this way then feature scaling becomes very important.
정규 방정식(Noraml Equation)
-
경사 하강법 외에 비용 함수를 최소화하는 분석적인 방법으로, 행렬 연산을 이용한다.

-
반복이 없다는 장점이 있지만 역행렬을 구하는데 연산이 많이 든다는 단점이 있다.

-
역행렬이 존재하지 않는 경우: 선형 대수에서는 역행렬이 존재하려면 행 벡터(row vector) 또는 열 벡터(column vector)끼리 선형 독립이어야 한다. 선형 독립이 아닌 경우는 첫번째 열 벡터가 두번째 열벡터의 2배 (v1 = 2*v2) 처럼 다른 벡터와 의존성이 있는 경우인데 이는 데이터셋에서 보기 힘든 케이스이다. 예를 들어 집을 m^2과 feet^2 으로 표현된 데이터셋이 있다고 하면 둘은 선형독립이 아니지만 데이터의 의미가 같으므로 하나의 열은 없애버려도 될 것이다. 이런 식으로 전처리를 하고 입력으로 주어지는 경우가 많기 때문에 역행렬이 존재하지 않는 경우는 거의 없다.
noninvertible, the common causes might be having :
Redundant features, where two features are very closely related (i.e. they are linearly dependent)
Too many features (e.g. m ≤ n). In this case, delete some features or use "regularization" (to be explained in a later lesson).
Solutions to the above problems include deleting a feature that is linearly dependent with another or deleting one or more features when there are too many features.
-
정규 방정식과 경사 하강법과의 비교: 데이터셋의 크기가 10^6 을 넘어가면 경사 하강법을 적용해야 한다.

'Machine Learning > Theory' 카테고리의 다른 글
| [비지도 학습 01] 클러스터링: K-means (0) | 2021.02.13 |
|---|---|
| [지도 학습 02] 로지스틱 회귀 (0) | 2021.02.09 |
| [심층 학습 03] 학습에 영향을 주는 요소 (0) | 2021.02.08 |
| [심층 학습 02] 역전파법(Backpropagation) (0) | 2021.02.07 |
| [심층 학습 01] 신경망(Neural Network) (0) | 2021.02.07 |