Move Fast

정보의 흐름

- 정보가 네트워크를 통해서 어떻게 흘러가는가?

• 구조적으로 노드들의 유일한 역할은 무엇인가?
• 다른 링크들(short vs long)은 무슨 역할을 하는가?

- 예제: 사람들은 새로운 직업에 대해 어떻게 발견하는가?

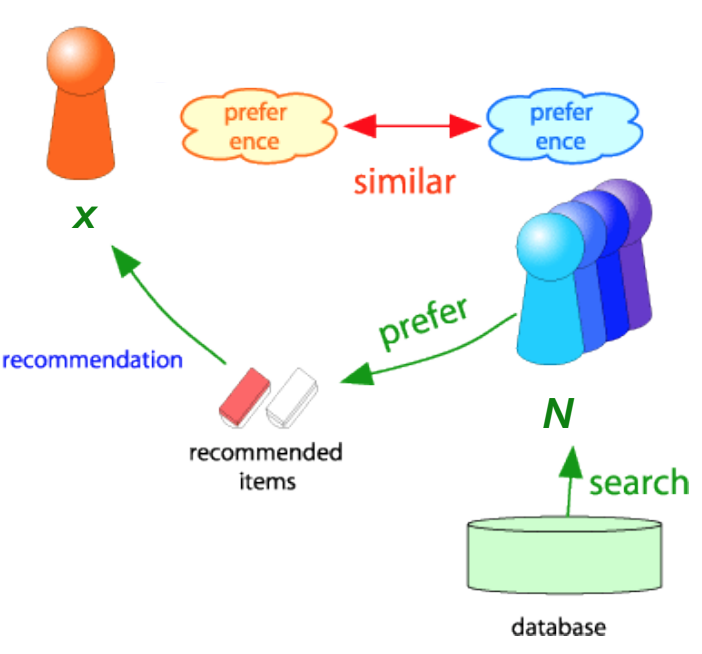
• 사람들은 개인적인 연락을 통해서 정보를 찾는다.
• 그러나, 연락(Contacts)은 종종 친한 친구들보다 지인(acquaintances)이었다.
• 왜 지인이 친구보다 더 도움이 되는가?
• Friendship 에 대한 두 가지 관점
  • Structural: Friendship 은 네트워크의 다른 부분을 span 한다.
  • Interpersonal: 두 사람 사이의 Friendship 은 strong 또는 weak 중 하나이다.
• 구조적 역할(Structural role): Triadic Closure
  • 한 네트워크에서 두 사람이 공통적으로 한 명을 친구로 두면, 두 사람이 친구일 확률이 높아진다.

b랑 친해질 확률이 더 높다.

- Granovetter의 설명: edge의 사회적, 구조적 역할 사이에 연결을 만든다.

• First point
  • 구조적으로 내재된 edge들은 사회적으로 강하다.
  • 네트워크의 다른 부분을 spanning하는 edge들은 사회적으로 약하다.
• Second point
  • 긴 범위의 edge는 네트워크의 다른 부분으로부터 정보를 얻도록 해주며, 일(job)을 얻도록 한다.
  • 구조적으로 내재된 edge들은 정보의 접근 측면에서 강하게 중복된다.

- Triadic closure == High clustering(community) coefficient

- Reasons for triadic closure: 만약 B와 C가 친구 A를 공통으로 갖는다면

• B는 C와 만날 확률이 높다. (A와 함께 시간을 보내기 때문에)
• B와 C는 서로 신뢰(trust)한다. (그들이 공통적인 친구를 갖기 때문에)
• A는 B와 C를 함께 데려오기 위한 동기(incentive)를 갖는다.
  • A는 두 분리된 관계를 유지하는 것을 힘들어 할 것이다.
  • 친구를 독점하는 경우는 거의 없음

- 개념

• Bridge edge: 제거되면 그래프는 연결이 끊어진다.(disconnect)
• Local bridge: Edge of Span(끊어졌을 때 돌아가는 거리의 길이) > 2 인 경우
• Edge는 두 개의 유형을 갖는데, Strong과 Weak 이다.
• Strong triadic closure: 두 strong tie들은 세번째 edge를 암시한다.
  • strong triadic closure는 local bridge가 weak tie임을 만족시킨다.

- Local Bridges 와 Weak ties

• 노드 A가 Strong Triadic Closure를 만족하고 적어도 2개의 strong ties에 포함된다면, A에 인접한 어떤 local bridge든 weak tie가 되어야만 한다.
• 결국 3개의 노드 모두 연결되어 있어야 한다.
• 대우명제(Proof by contradiction)
  • 노드 A가 Strong Triadic Closure를 만족시킨다.
  • A와 B 사이에 local bridge가 있고 strong tie라고 가정하자.
  • B와 C 사이에 edge는 존재해야 한다. (Strong Triadic Closure 이므로)
• 그러나, B와 C 사이에 strong edge가 없으므로 모순이다. A와 B 사이에는 weak tie 만 존재할 수 있다.

- 실제 데이터에서 Tie strength

• who-talks-to-whom graphs: email, messenger, cell phone, facebook

- Neighborhood Overlap

• Edge overlap = Oij = N(N(i)∩N(j)) / N(N(i)∪N(j)) = 교집합 크기 / 합집합 크기
• N(i) = 노드 i의 이웃 노드들의 집합
• Overlap = 0 → edge는 local bridge 이다.

빨간색일수록 이웃이 많이 겹치는 걸 의미

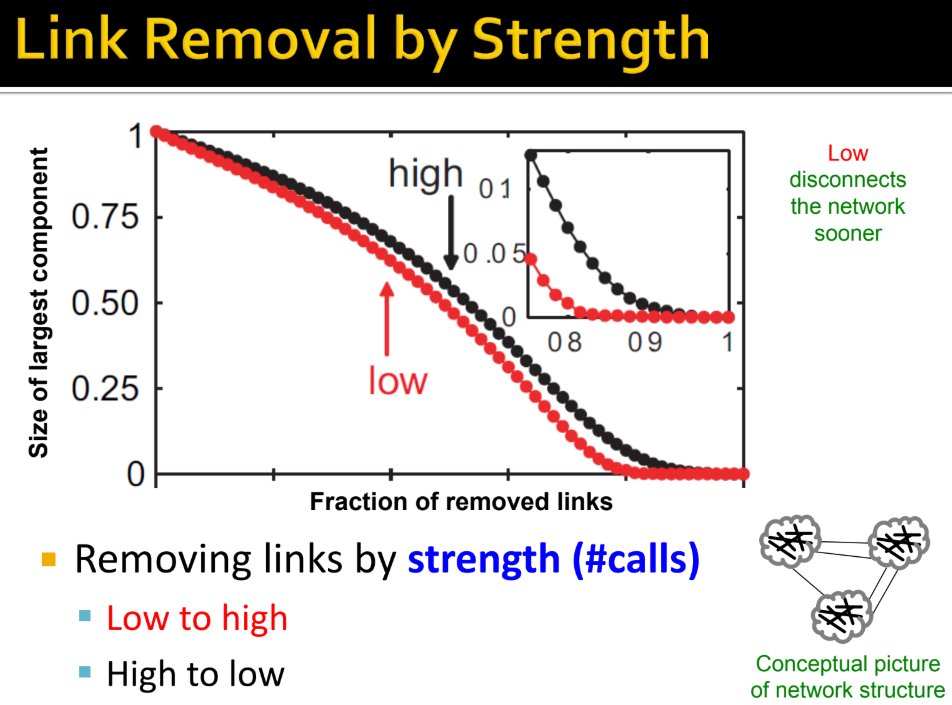
• Low → 겹치는 이웃이 적어지는 것을 의미
• Low to high → 이웃이 적게 연결된 링크(이전 예시에서 노란 선)부터 끊는 경우
• High to low → 이웃이 많이 연결된 링크(이전 예시에서 빨간 선)부터 끊는 경우

- weak ties 는 edge overlap 이 낮고, strong ties 는 높다.

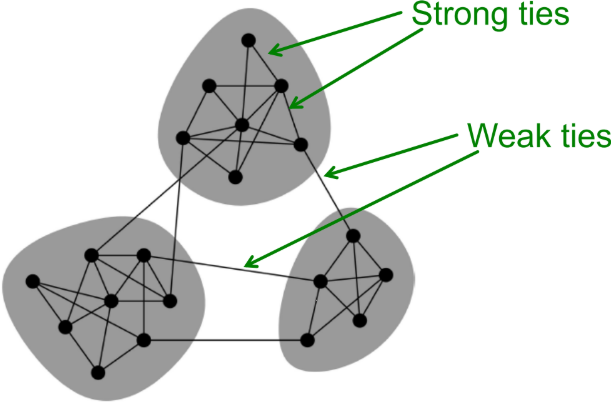
네트워크 커뮤니티(Network Communities)

- Granovetter의 이론에 따르면, 네트워크는 노드들의 단단히(tightly) 연결된 집합들로 구성되어 있다.

- 내부 노드는 많이 연결되어 있어야 하고, 나가는 링크는 적어야 커뮤니티가 형성된다.

- communities, clusters, groups, modules 모두 같은 말

- 이상적으로, 자동으로 발견된 클러스터들은 실제 그룹과 대응한다.

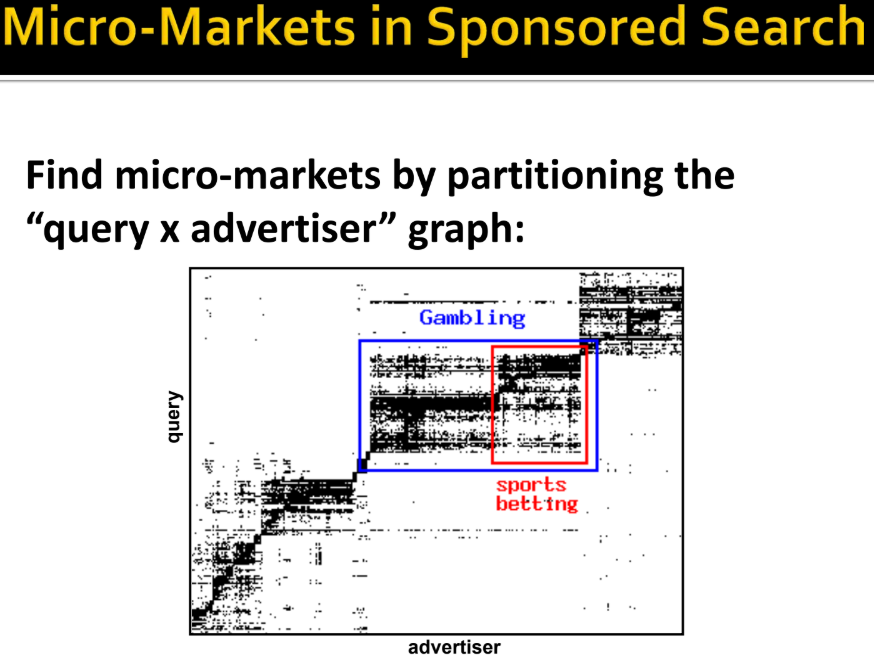
- 소셜 네트워크 데이터: 아래의 빨간선은 cross link가 가장 적은 부분으로, 실제 관계가 좋지 않았다고 밝혀졌다.

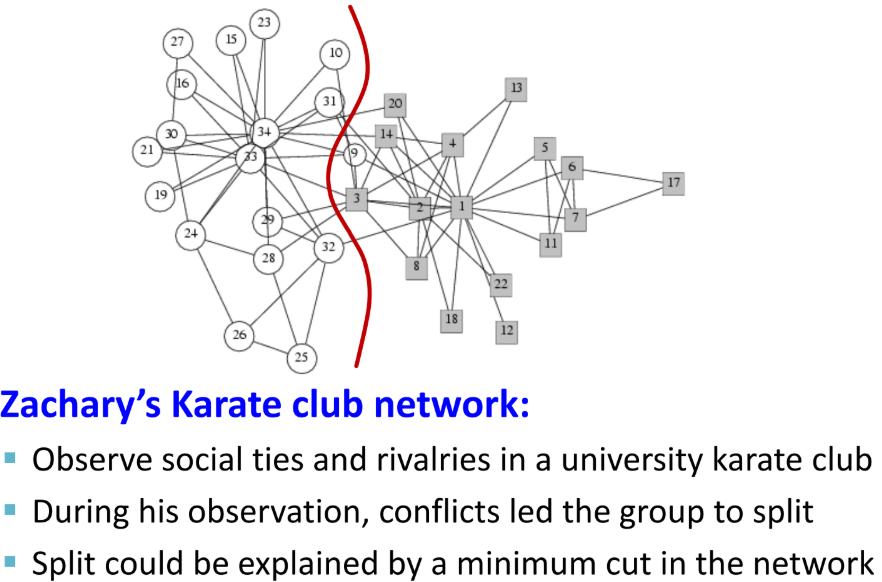
커뮤니티 탐색(Community Detection)

- 방법1

• strength of Weak Ties
  • Edge betweenness: 그 edge를 지나는 가장 짧은 경로의 개수
  • betweenness 가 높으면 edge strength 와 edge overlap 은 낮다.

b = 4 * 4 = 16 → 모든 노드가 지난다.

b = 5 * 3 / 2 = 7.5 → 오른쪽 edge는 위에 겹치는 edge가 하나 더있어서 2로 나눔

• Girvan-Newman: edge betweenness 기반의 분할 계층적 클러스터링
  • 커뮤니티를 찾을 때, 모든 edge에 대해 edge betweenness를 계산한 뒤 가장 높은 것부터 끊는 방법으로, edge가 모두 없어질 때까지 반복한다.
  • 이후 남은 Connected component들은 모두 커뮤니티이다.
  • 네트워크의 계층적 분해

12 = (2*12)/2, 33 = 3*11, 49 = 7*7

edge of 12 는 1번 노드에 연결된 노드가 2번 노드만 있으므로 수치 2에다 3번 노드에 연결된 노드의 개수가 12개이므로 12를 곱한다. 그 뒤, 2-3번 노드가 유사한 역할을 수행하는 edge이므로 중복 제거를 위해 2를 나눠준다. edge of 33은 3번 노드에 자기 포함 노드가 3개 있고7번 노드에는 자기 포함 11개의 노드가 연결되어 있으므로 3*11 이다. 나머지도 마찬가지

• Step 1: 가장 값이 큰 edge of 49 부터 끊는다.
• Step 2: 그 다음으로 큰 edge of 33을 모두 끊는다.
• Step 3: 그 다음으로 큰 edge of 12를 모두 끊는다.

Edge betweenness를 계산하는 방법

- 시작 노드를 root로 두고 깊이 우선 탐색을 수행

- 시작 노드로부터 같은 네트워크의 다른 모든 노드까지 가장 짧은 경로 개수를 알아낸다.

- A에서 특정 노드 X까지 가는 경로의 개수 = A에서 X의 부모 노드까지 가는 경로의 개수의 합

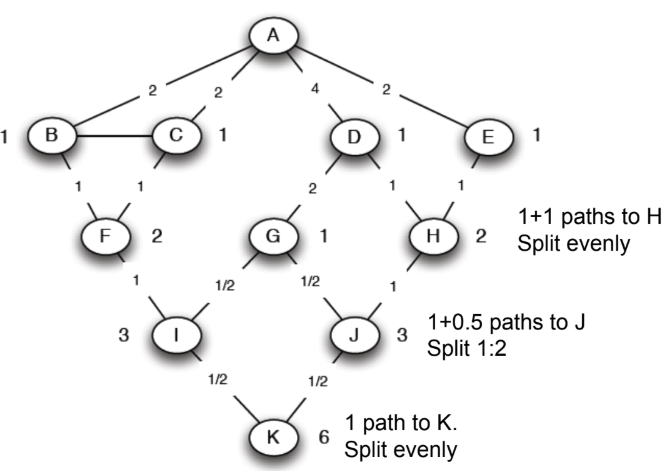
- 가장 밑에 있는 자식 노드부터, betweenness를 계산해서 부모 노드로 분배한다.

• node flow = 1 + (자식 노드의 edge betweenness의 합)
  • 가장 밑의 자식 노드는 자식이 없으므로, node flow는 1이다.
• 부모 노드의 경로 개수를 비율로 node flow를 분배한다.
  • 예를 들어, K는 node flow 가 1이다. 노드 K의 부모 노드 I와 J의 경로 개수 비율이 3:3=1:1이므로 1을 나누면 각각 ½ 씩 betweenness를 갖게 된다. 노드 J는 자식 노드가 K만 있으므로 node flow = 1 + ½ =1.5 가 되며, 부모 노드 G와 H의 경로 개수 비율이 1:2이므로 1.5를 나누면 각각 0.5, 1을 betweenness로 갖게 된다.
• root 노드까지 위의 과정을 반복한다.

- 모든 노드를 시작 노드로 두고, 경로의 개수를 계산한 뒤 위의 과정을 반복한다.

클러스터의 개수를 선택하는 방법

- 네트워크 커뮤니티는 단단히 연결된 노드의 집합이다.

- Modularity Q = 네트워크가 커뮤니티로 얼마나 잘 분할되었는지 측정하는 척도

• group s ∈ S 일 때,아래의 식이 성립한다.

• 그룹 S 내 모든 작은 그룹의 (그룹 내 edge의 개수) - (그룹 내 edge의 개수 기댓값)의 합은 Q와 비례한다.

- Null Model: Configuration Model

• n개의 노드와 m개의 edge를 가진 그룹 G가 주어졌을 때, 네트워크 G`은 다음 사항대로 네트워크를 다시 형성한다.
  • 동일한 degree 분배이지만 무작위로 연결한다.
  • G`을 multigraph로 여겨야 한다.
  • degree가 ki이고 kj인 노드 i와 j의 edge betweenness의 기댓값(expected number)은 다음과 같다.

- 그래프 G의 일부인 C의 Modularity

- Modularity 값은 [-1, 1]의 범위를 가진다.

• 그룹 내 edge의 숫자가 기댓값보다 크면 좋다.

• 0.3 < Q < 0.7 은 거대한 커뮤니티 구조를 의미한다.

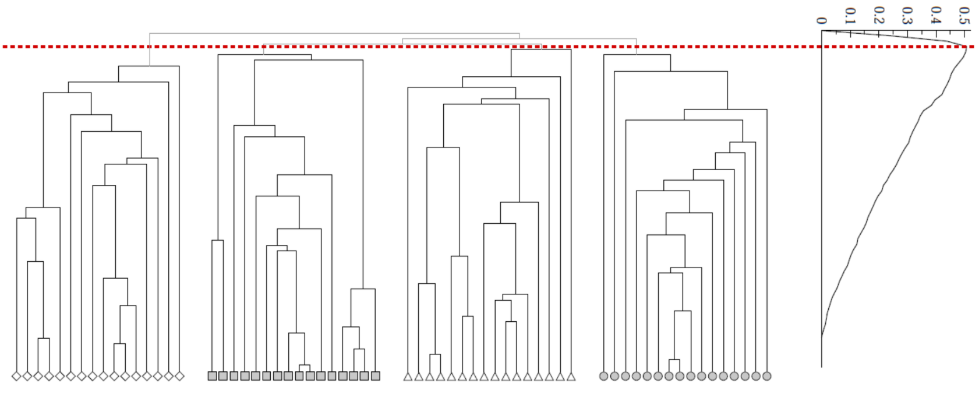
- Modularity는 클러스터 개수를 선택하는 유용하다.

• 아래 예시에서 적절한 커뮤니티의 개수는 4개이다.

부호있는 Edge를 가진 네트워크(Networks with Signed Edges)

부호있는 네트워크(Signed Networks)

- 양(positive)의 관계, 음(negative)의 관계를 가진 네트워크: 기본 조사 단위는 부호 있는 삼각형(signed triangles)인데, 먼저 방향성(undirected/directed)에 대해서 언급을 해야 한다.

- Plan

• Model: 부호있는 네트워크의 두 가지 사회적 이론
• Data: 큰 온라인 네트워크의 존재 이유
• Application: A와 B가 양의 관계 또는 음의 관계로 링크되어졌는지 예측

- Undirected complete graph: 각 edge는 레이블이 붙는다.

• Positive: friendship, trust, positive sentiment, …
• Negative: enemy, distrust, negative sentiment, …

구조적 밸런스 이론(Theory of Structural Balance)

- 직관적으로, 내 친구의 친구는 친구이다. 적의 적도 친구이다. 적의 친구는 나의 적이다.

- Unbalanced 를 보면, 나의 친구의 친구가 나와 음(-)의 관계임을 알 수 있다. 이는 불균형한 상태이며 일관적이지 않다(Inconsistent).

- 음(negative)의 개수가 홀수(odd)이면 불균형(Unbalanced) 상태이고, 짝수(even)이면 균형(Balanced) 상태이다.

- 모든 3개의 edge는 양(+)의 관계로 레이블되어져 있거나 정확히 1개의 edge만 양(+)의 관계로 레이블되어있고 연결되어 있으면 균형잡힌 그래프(Balanced Graph)이다.

- 불균형한 그래프(Unbalanced Graph)를 하나라도 포함하면 전체 그래프도 불균형하다.

- Local Balance → Global factions

• 균형(Balance)은 전역적인 연합(global coalitions)을 의미한다.
• 만약 모든 삼각형이 균형잡힌 그래프라면, 그 네트워크는 양의 관계(positive edge)만 가지거나, 노드들이 오로지 음의 관계(negative edge)를 갖는 2개의 집합으로 분리될 수 있다.

• 그룹간 음의 관계(negative)는 최대 1개만 갖도록 하는 방법인데, 그룹 내에는 양의 관계(positive)만 존재하거나 하나도 없어야(음의 관계만 있다면!) 한다.

- Analysis of Balance

- 예제: 국제 관계

• 국가 간 주변국에 대한 찬반이 존재 → 1971년 파키스탄으로부터 방글라데시의 독립 문제로 미국이 파키스탄을 지원하는지 예측하는 것

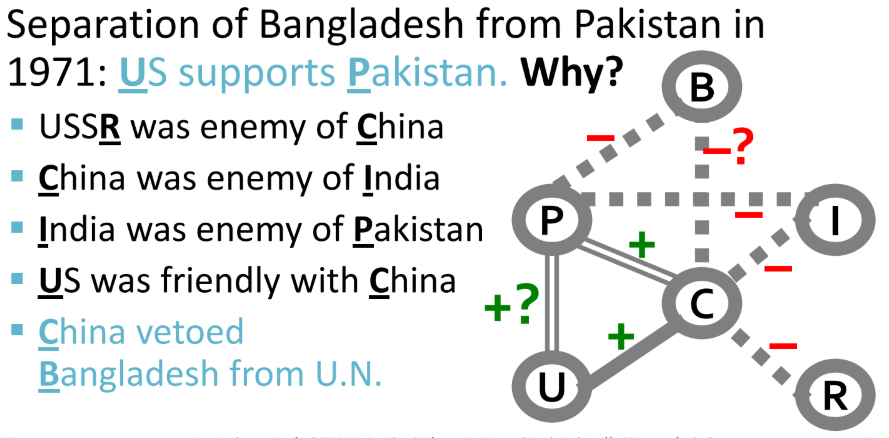
• R(미국)과 C(중국)은 적대관계이고, C(중국)은 I(인도)와 적대관계이고, I(인도)는 P(파키스탄)과 적대관계이다. U(미국)는 C(중국)와 친한 관계이므로, C(중국)와 친한 P(파키스탄)을 지원(+)해줄 것이다.
• B(방글라데시)는 P(파키스탄)과 적대관계이므로 C(중국)도 B(방글라데시)를 적으로 둘 것이다.

일반적인 네트워크에서의 균형(Balance in General Networks)

- 이전까지는 complete graph에 대해 다루었다.

- 지역적 관점(Local view): 균형을 잡기 위해 없는 edge를 채워보는 것

- 전역적 관점(Global view): 그래프를 두 개의 연합(coalition)으로 나누는 것

- 위의 두 관점은 필요 충분 조건이다.

- 그래프가 균형(balanced) 상태이면, 반드시 음의 관계(negative edges)를 홀수개 가진, 어떤 싸이클도 없어야 한다.(no cycle)

- 계산하는 방법

• 양의 관계(+ edges)를 가진 connected components 찾기
  • 만약 음의 관계(- edges)를 포함한 양의 관계(+ edges)를 가진 노드들의 component를 발견한다면, 이는 불균형이다.
• 각 component에 대한 슈퍼 노드(super node)를 생성한다.
• 슈퍼 노드의 멤버 사이에 음의 관계(- edges)가 있다면, 2개의 component 로 연결한다. 그러면 2개의 component가 각각의 슈퍼 노드가 된다.
• 슈퍼 노드를 BFS를 이용해서 편을 나누면 된다.

음의 관계가 짝수개이면 편가르는게 가능하다. 홀수개는 분할 할 수 없다.

쉽게 말하자면, 양의 관계(+ edges)로 연결되거나 아무것도 없는 노드들만 찾아서 그룹화

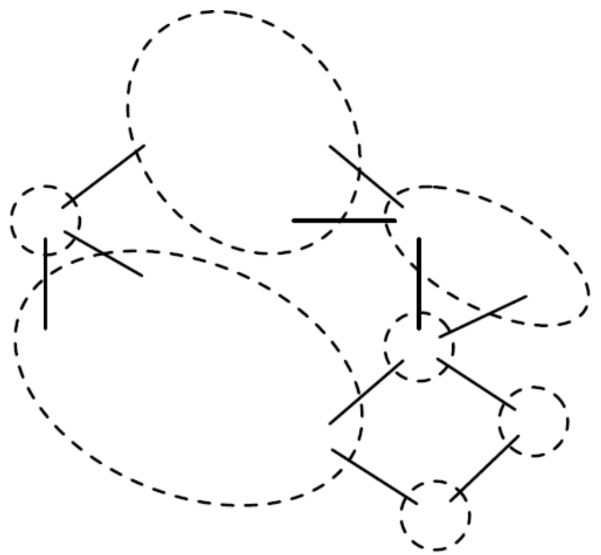
각 component의 그룹이 슈퍼 노드가 되었다. (왼쪽에 7개의 슈퍼노드가 존재)

그러나, 중복되는 edge가 존재하므로 불균형 상태이다. 따라서 중복되는 edge를 제거해준다.

BFS를 이용해서 각 슈퍼 노드 나누었는데, 어떤 두 슈퍼 노드들이 같은 편(side)에 할당되면 불균형 상태이다.

네트워크의 구조

- 네트워크란 링크에 의해 연결된 개체 쌍들이 있는 객체들의 집합

- 네트워크 구조

• Objects: nodes, vertices → N
• Interactions: links, edges → E
• System: network, graph → G(N, E)

- 네트워크는 종종 실제 시스템을 표현한다. 예를 들어, 웹(Web), 소셜 네트워크(Social network), Metabolic network 가 있다.

• Network, node, link

- 그래프는 네트워크의 수학적인 표기법이다. 예를 들어, 웹 그래프(Web graph), 소셜 그래프(Social graph in facebook)이 있다.

• Graph, vertex, edge

적절한 표현의 선택

- 적절한 네트워크 표현법을 선택하는 것이 성공적으로 네트워크를 사용하는 능력을 결정한다.

• 몇몇 경우에 유일하고 모호하지 않은 표현법이 있다.
• 다른 경우에 그 표현법이 결코 유일하지 않다.
• 링크를 할당하는 방식이 공부할 질문의 본질을 결정할 것이다.

- 서로서로 동작하는 개체를 연결하면, 전문적인 네트워크(professional network)를 탐구할 것이다.

- 성적 관계를 가지는 사람들을 연결해보면, 성적인 네트워크(sexual networks)를 탐구하고 있을 것이다.

• 예를 들어, 사람들의 관계를 표현했을 때 중간 노드는 성병에 걸리면 안쪽으로 퍼져나갈 수 있어서 실제 성병에 걸리면 안되는 경우 등을 판단할 수 있다.

- 서로서로 인용하는 논문들을 연결해보면, 인용 네트워크(citation network)를 공부할 것이다.

Undirected vs Directed Networks

- Undirected Example: Collaborations, Friendship on Facebook, 상호간의 동일한 관계

- Directed Example: Phone calls, Following on Twitter, 비대칭적인 관계

그래프의 연결성(Connectivity of Graphs)

- Connected Component: 연결된 노드의 집합

- Connected (undirected) graph: 방향성 없이, 모든 노드가 연결되어 있는 그래프 (Connected Components가 존재하지 않음)

- Disconnected (undirected) graph: 방향성 없이, 둘 이상의 connected components가 존재

여기서 H 노드 하나만 보면 connected components로 볼 수 있다.

- Bridge Edge: 제거되면, connected component 개수가 늘어나는 edge

- Articulation point: 제거되면, disconnected graph가 되버리는 node(point)

- Connected (directed) graph: 두 노드간 이동이 가능한 방향이 존재하며, 각 노드로부터 모든 노드로 이동할 수 있는 경로가 존재하는 그래프

- Weakly connected directed graph: 그래프 중 모든 노드가 연결된 그래프 (양방향으로 도달되지 않는 노드들이 존재)

그래프로서의 웹

- Nodes = web pages

- Edges = hyperlinks

- 초기 웹 링크는 방향을 알려주는 역할(navigational)이었다.

- 오늘날 많은 링크는 교류하는 역할(transactional)이다.

- Web as a directed graph: 노드 v가 주어졌을 때 들어오는 링크는 incoming link, 나가는 링크는 outcoming link로 정의된다.

- Directed Graph

• Strongly connected: 어떤 노드도 다른 노드에 도달할 수 있는 path가 존재
  • In Set = Out Set (동일)

• Directed Acyclic Graph(DAG): 사이클이 없는 그래프, 노드 u는 v에 도달해도 노드 v는 u에 도달하지 않음

Strongly Connected Component (SCC)

- 집합 S에서 노드들의 모든 쌍이 서로 도달할 수 있다.

- SCC이면서 집합 S를 포함하는 더 큰 집합은 존재하지 않는다.

- 예제: {A, B, C}는 첫번째 조건을 만족하나, {A, B, C, G}가 존재하므로 두번째 조건은 만족하지 못한다. (not SCC)

- 모든 directed graph 는 SCC들의 DAG이다. 즉, 모든 쌍들이 서로 도달할 수 있는 작은 그래프들이 모인 것이라고 볼 수 있다.

• SCC는 그래프 G의 노드들을 분할한다.(partition) → 각 SCC를 노드로 본다.
• SCC를 노드로 보는 그래프 G`이 있을 때, G`은 DAG 이다.

- 증명1: SCC는 그래프 G의 노드들을 분할한다. 각 노드는 정확히 1개의 SCC의 멤버이다.

• 대우명제(Proof by contradiction): 2개의 SCC를 가지는 그래프 S와 S`이 있을 때, 두 그래프에 동시에 멤버가 되는 노드 v가 존재한다. 그러나, S와 S`의 합집합은 하나의 큰 SCC가 된다. 이것은 모순이다.

- 증명2: SCC들의 그래프 G`은 DAG 이다. G`에는 사이클(cycle)이 없다.

• 대우명제(Proof by contradiction): 그래프 G`이 DAG가 아니라고 가정했을 때, G`은 directed cycle을 가진다. cycle 에 있는 모든 노드들은 서로 도달가능하며 같은 SCC의 일부이다. 그러나 G`은 SCC 사이에 순환가능한 그래프가 아니다. SCC는 최대 순환가능한 노드의 집합으로 정의되므로 이는 모순이다.

웹에서의 그래프 구조

- 웹의 큰 스냅샷을 살펴보면, 어떻게 SCC들이 DAG로 서로 맞춰있는지 이해할 수 있다.

- Computational Issues: SCC가 노드 v를 포함하는 것을 어떻게 발견?

• In(v): 노드 v로 들어오는 노드들의 집합
• Out(v): 노드 v로부터 도달가능한 노드들의 집합
• SCC 에 노드 v가 포함되면, Out(v)와 In(v)의 교집합에 노드 v가 있다.
• 단, 위의 방법은 연산이 많이 걸리므로 Out(v,G)와 Out(v, 방향을 뒤집은 G)의 교집합으로 노드 v를 찾는다.

전체 SCC의 개수는 {A, B, D, E, F, G} 와 {C}로 2개이다.

- 웹은 매우 큰 SCC 이다. 2개의 매우 큰 SCC는 존재하지 않을 것이다.

- 귀납적 논쟁

1. 하나의 SCC에서 다른 SCC로 가는 link는 1 페이지만 소요된다.
2. 만약 2개의 SCC가 몇 백만 페이지를 가진다면, 이 일이 일어나지 않을 가능성은 매우 적다.

웹의 구조

- 초기 웹은 데이터베이스에 링크나 url을 저장해둔 형태로 서버는 12GB의 메모리를 가졌었다.

- Undirected version of the Web graph

• 가장 큰 weakly connected component 에서 91% 노드가 존재
• hubs는 웹 그래프를 연결되도록 했는가?
  • 들어오는 link의 개수(in-degree) > 10 인 페이지들에 대한 link를 삭제한다면 WCC는 여전히 그래프의 50%가 남아있다.

- Directed version of the Web graph

• 가장 큰 SCC: 노드들 중 28%가 해당된다. (56 million)
• 랜덤으로 노드 v를 가져오는 것은 Out(v) ~ 50% (100 million), In(v) ~ 50% (100 million) 이 되게 한다.
  • 즉 성능이 랜덤으로 가져오는게 더 좋다.

Conceptual Organization (ex: bowtie)

개념 (Concept)

- 군집 분석(Cluster analysis)은 비지도 학습으로, 지도 학습이 분류(Classification)를 위해 미리 레이블(label)되어 있어 전문가(해당 데이터셋에 대한 분석이 필요, 레이블의 의미 등)의 도움이 필요하다는 점에서 차이가 있다. 그러나 군집 분석도 큰 데이터 집합(a cloud of data points)이 주어지면 그 구조를 이해해야 한다.

- 점들의 집합(set of points)이 주어지면, 점들간의 거리를 이용하여 몇 개의 클러스터로 그룹화를 해야 한다.

• 클러스터 내 점들은 서로 가까워야(유사해야) 한다.
• 다른 클러스터의 점들은 거리가 멀어야(유사하지 않아야) 한다.

- 보통 점들은 고차원 공간에 있다. → 데이터 집합에서 feature 가 많다. → 차원 축소 (필요 없는 feature 걸러내기)

- 유사도(Similarity)는 거리 척도를 이용해서 정의된다.

• Euclidean
• Cosine
• Jaccard
• edit distance (두 문자열 사이의 거리 = 몇 개를 바꿔야 그 문자열이 되는가?)

- Outlier 는 어느 클러스터에도 속하지 못하는 점으로, 탐지가 어렵다.

- 2차원에서의 클러스터링은 쉬워보인다. 데이터가 적은 양을 클러스터링하는 것은 쉽기 때문이다.  그러나, 많은 경우 2차원이 아닌 10차원 혹은 10,000 차원에 해당된다.

- 고차원 공간은 다르게 보기 → 대부분 점들은 모여있어서 특정 점으로부터 같은 거리에 있다.

- 예제: 음악 CD → 직관적으로, 음악은 카테고리로 분류되고, 고객들은 몇 가지 카테고리를 선호한다.

• 접근: 비슷한 CD(같은 카테고리)를 구매한 고객들의 집합으로 CD를 표현
• 비슷한 사람들이 구매했을 것
• 유사한 CD는 유사한 고객들의 집합을 가진다. 역도 성립
• 모든 CD의 공간: 1차원의 공간으로 생각하면, 각 고객에 대해 차원 내 값은 0~ 1사이 일지도 모른다. 하나의 CD는 이 공간 내 점이다. (X, X, …, Xk) 여기서 Xi=1 이면 i번째 고객이 CD를 구매한 것이다. → 유사한 CD를 그룹화하는 클러스터 찾는 것이 해야할 일이다.

- 예제: 문서(Documents) → 주제 찾기

• 벡터로 문서를 표현 → (X1, X2, …, Xk)
• 여기서 Xi는 i번째 단어가 그 문서에 나타났음을 의미한다. k가 무한한 것은 중요하지 않다. (단어의 집합을 제한하지 않음)
• 유사한 단어의 집합을 가진 문서는 같은 주제일 것이다.

- 거리 개념: Cosine, Jaccard, and Euclidean

• Sets as vectors: 유사도는 Cosine distance 로 표현된다.

• Sets as sets: 유사도는 Jaccard distance 로 표현된다.

• Sets as points: 유사도는 Euclidean distance 로 표현된다.

클러스터링 방법

- 계층 구조(Hierarchical)

• Agglomerative → Bottom up: 초기의 각 점은 클러스터이다. 반복적으로 두 개의 가까운 클러스터를 하나의 클러스터로 결합한다. 이를 반복

• Divisive → Top down: 하나의 클러스터를 2개씩 나눈다. 이를 반복

- Point assignment: 이미 있는 클러스터들 중 새로운 점을 가장 가까운 클러스터에 할당한다.

계층적 클러스터링(Hierarchical Clustering)

- 핵심 연산: 가장 가까운 클러스터끼리 반복적으로 결합하는 것

- 고려 사항

• 클러스터간 거리는 어떻게 표현?
  • 각 클러스터의 위치를 정의
• 가까움(nearness)을 어떻게 결정?
• 클러스터 결합을 언제 멈춤?

- centroid = 클러스터 내 점들의 평균 (포함된 점이 아닐 수 있음, 즉 좌표)

• 가까움은 centroid 의 Euclidean distance 로 정의된다.

o = data point, x = centroid

- clustroid = 클러스터 내 점들과 가장 가까운(closest) 점

• 가까움은 clustroid 의 Euclidean distance 로 정의된다.
• closest 의 다양한 의미
  • 다른 점들에 가장 작은 최대 거리
  • 다른 점들에 가장 작은 평균 거리
  • 다른 점들에 가장 작은 거리제곱합(Sum of squares of distances)

- 그 외 가까움을 정의하는 방법

• Intercluster distance = 각 클러스터에서 클러스터 내 두 점들 사이에 거리의 최솟값
• 클러스터의 cohesion 의 표기법을 선택, 즉 clustroid 에서 최대 거리
• 병합된 클러스터의 diameter 를 사용 → 클러스터에서 점들 사이의 최대 거리
• 클러스터에서 점들 사이에 평균 거리를 사용
• 밀집도(density) 기반의 접근법 → diameter 또는 평균 거리를 구한 뒤, 클러스터 내 점들의 개수로 나눔

- 구현

• 각 단계에서, 클러스터의 모든 쌍 사이에 거리를 계산하고 결합
• O(N^3) → 우선순위 큐를 사용하면 O(N^2*logN)으로 줄일 수는 있다.
• 그러나 여전히 비용이 비싸다.

k-평균 클러스터링(k-means clustering)

- Point assignment 의 대표적인 방법으로, 여기서 k는 클러스터의 개수를 의미한다.

- 알고리즘

• 유클리디안 공간이나 거리를 가정한다.
• 클러스터 개수 k를 선택
• 클러스터별 하나의 점(centroid 역할)을 선택해서 클러스터를 초기화한다.
  • 랜덤으로 k번째 점을 고르는 방법, 여기서 k-1개의 다른 점들은 이전 점들과 가능한 멀리 떨어져 있다.
• 각 점을 그 점과 가장 가까운 centroid를 갖는 클러스터에 포함시킨다.
• 모든 점들이 할당된 후, k개의 클러스터들의 centroid의 위치를 갱신한다.
• 모든 점들을 가장 가까운 centroid를 갖는 클러스터로 재할당한다. 여기서 클러스터 내 점들이 바뀔 수 있다. 이를 클러스터의 변화가 없을 때(convergence = 점들이 움직이지 않음)까지 반복한다.

- 클러스터 개수 선택: 클러스터 개수를 1개씩 늘리면서 centroid 간의 평균 거리가 더 이상 많이 감소하지 않는 경우의 k를 선택한다. 개수가 늘 때마다 평균이 급격히 감소하는데 적절한 k가 발견되면 매우 천천히 감소한다.

- 클러스터 개수가 적으면, centroid 의 거리가 매우 길다. 적절한 개수이면 거리가 점점 짧아진다. 개수가 많으면, 평균 거리가 매우 조금씩 줄어든다.

Bradley-Fayyad-Reina (BFR) Algorithm

- 매 반복마다 거리를 계산한다면, 디스크 입출력(메인 메모리에 데이터를 많이 못올리는 경우) 시 데이터가 많을수록 비효율적이다.

- 매우 큰 데이터 집합을 다루기 위해 설계된 k-means의 확장버전

- 유클리디안 공간에서 클러스터들이 보통 centroid 주변에 분산되었다고 가정

• 다른 차원에서의 표준 편차는 다양할 수 있다. → x축, y축으로 볼 때 각 그래프를 보는 관점이 다름
• 2차원 그래프에서는 표준편차가 높을수록 넓은 산 모양이고, 낮을수록 좁은 산 모양이다.

- 클러스터를 모으는 효율적인 방법

• 데이터를 묶어서 단위별로 메모리에 로드시킨 후, 특징을 추출(통계적 연산)하고나면 디스크로 보내고 새 묶음을 다시 로드

- 시작할 때, 초기 로드 시 최초의 k를 선택할 때 접근법

• k 개의 점들을 랜덤으로 선택
• 선택적으로 작은 랜덤 샘플과 클러스터를 선택
• 샘플을 선택하면, 랜덤으로 점을 선택한 뒤 k-1 개의 다른 점들은 이전에 선택된 점들로부터 가능한 멀리 떨어져 있어야 한다.

- 점들의 3개의 클래스

• Discard set (DS): 합쳐질, centroid에 충분히 가까운 점들의 집합
• Compression set (CS): 어떤 centroid에 가깝지 않고 서로 가까운 점들의 집합, 이 점들은 합쳐지지만 하나의 클러스터로 할당되지는 않는다.
• Retained set (RS): compression set으로 할당되어지기를 대기하는 고립된 점들의 집합

- 점들의 집합을 합치는 법: 각 점들에 대해, discard set (DS) 이 다음 사항에 의해 합쳐진다.

• N = 클러스터 내 점들의 개수
• SUM = i번째 요소는 i차원에서 점들의 좌표(coordinates)의 합을 의미하는 벡터
• SUMSQ = i번째 요소는 i번째 차원에서 좌표의 제곱의 합을 의미하는 벡터

- 점들의 집합을 설명하는 법

• 차원 수가 d라고 정의될 때, 각 클러스터의 크기는 2d + 1 로 표현된다.
• 각 차원에서 평균은 SUMi/N 으로 계산된다. 여기서 SUMi는 벡터 SUM의 i번째 요소
• i 차원에서 클러스터의 discard set (DS)의 분산은 (SUMSQi / N) - (SUMi / N)^2 으로 정의된다.
• 표준편차는 위에서 구한 분산의 제곱근

- 메모리 로드하는 법

• centroid 에 충분히 가까운 점들을 찾고, DS와 클러스터에 그 점들을 추가
• 오래된 RS에 남은 점들을 군집화하기 위한 메인 메모리 상의 클러스터링 알고리즘을 사용
  • 클러스터들은 CS로 가고, outlier 들은 RS로 이동
  • RS는 다음 반복에서 사용된다.
• DS set: 새로운 점들을 설명하기 위해 클러스터의 통계적 연산을 적용 (N, SUM, SUMSQ)
• CS에서 압축될 집합(compressed sets)을 합병
• 마지막 반복인 경우, CS에서 모든 압축될 집합과 모든 RS 내 점들을 그것들의 가장 가까운 클러스터로 병합

- 해당 클러스터로 점을 추가할 그 클러스터에 충분히 가까운 것을 어떻게 결정?

• 새로운 점을 클러스터로 놓을 지를 결정할 방법이 필요한데, BFR은 2가지 방법을 제시
• Mahalanobis distance < threshold: centroid로부터 정규화된 유클리디안 거리 

• 만약 d 차원에 정규분포로 클러스터가 존재하면, 변형(trasformation) 이후, 표준편차는 sqrt(d)가 됨
• 즉, centroid에서 거리가 68% 정도 되면 같은 클러스터로 볼 수 있다.

• 현재 가장 가까운 클러스터에 속할 확률이 높은 점(높은 우도를 가진 점)

- 2개의 압축될 집합(CS)을 하나로 결합 할 지를 어떻게 결정?

• 결합된 subcluster의 분산을 계산 (N, SUM, SUMSQ 이용)
• 만약 결합된 분산값이 어떤 임계값보다 낮으면 결합 (분산 < 임계값)

Clustering-Using-REpresentatives (CURE) Algorithm

- BFR/k-means의 문제점

• 클러스터들이 각 차원에서 정규분포 형태라고 가정하고 알고리즘을 수행한다.
  • 그러나 대부분 데이터들이 정규분포가 아닐 수 있음
• 고차원 공간에서 각 축은 고정되어 있으나 타원(데이터가 모여서 만들어진 모양)의 각도는 그렇지 못하다.

- CURE 알고리즘 특징

• 유클리디안 거리를 가정
• 어떤 모양이든 클러스터링이 가능
• 클러스터를 표현하기 위해 대표적인 점들을 수집

- 2 Pass Algorithm: 첫번째 단계

• 메인 메모리에 맞는 랜덤 샘플(점들의 집합)을 선택
• 초기 클러스터는 계층적으로 점들을 군집화한다. 가장 가까운 점들, 클러스터들끼리 그룹화
• 대표 점을 선택: 각 클러스터에 대해, 가능한 흩어진 점들의 샘플을 선택한다.
• 해당 샘플로부터 클러스터의 centroid로 20% 씩 이동시키면서 대표 점을 수정하여 선택한다.

- 2 Pass Algorithm: 두번째 단계

• 전체 데이터 집합을 다시 스캔하고 데이터 집합에서 각 점 p를 방문한다.
• 가장 가까운 클러스터에 그 점을 놓는다.
  • 가까움의 일반적인 정의는 점 p에 가장 가까운 대표 점을 찾고, 대표점의 클러스터에 찾은 점을 할당하는 것
  • 초기에는 centroid 중심으로 정규분포화된 클러스터를 가정하고 이후 대표 점을 중심으로 점들을 옮긴다.
  • 다양한 형태가 나올 수 있다.

- 정리하자면, 클러스터링은 주어진 점들의 집합에서 점들간 거리를 정의하고 몇 개의 클러스터들로 점들을 그룹화한다.

차원 축소 (Dimensionality Reduction)

- 가정: 데이터는 d 차원의 서브공간에 놓이거나 근처에 있다.

- 서브공간의 축(axes)은 데이터의 대표 점에 영향을 준다.

- 차원을 압축하거나 축소하는 법: 두 벡터 [1,1,1,0,0] 과 [0,0,0,1,1] 로 아래의 데이터를 표현할 수 있다. (5차원 → 2차원)

왼쪽 좌표는 벡터 [1,1,1,0,0]과 [0,0,0,1,1]로 표현했을 때 각 customer의 2차원 공간에서의 좌표이다.

- 행렬의 rank: 행렬에서 선형 독립인 열의 개수 → Rank 는 차원(Dimensionality)이다.

- 행렬은 기저 벡터(basis vector) 로 표현할 수 있다.

위의 경우 (벡터 [1,2,1]의 개수, 벡터 [-2,-3,1]의 개수) 로 2차원 좌표로 표현 가능

- 차원 축소의 목표는 데이터의 축을 찾는 것이다.

- 2개의 좌표를 가지는 모든 점을 표현하기 보다, 1개의 좌표로 각 점을 표현하는 것이 낫다.

• 선형 회귀가 대표적인데, 여기서 직선과 점의 거리가 아닌 수선의 발을 이용한다. 연산이 용이하기 때문인데, 수선의 발 길이가 클수록 변화(오류)가 크다는 것을 의미한다.
• 각 점과의 오류가 가장 적은 선을 찾는 것이 핵심이다.

- 차원을 축소하는 이유

• 숨겨진 상관 관계(correlation)이나 주제를 찾기 위함
  • Text: 공통적으로 같이 쓰이는 단어들이 있다.
• 중복되거나 쓸모없는(noisy) 특징(feature)들을 제거하기 위함
  • Text: 모든 단어들이 유용하진 않다.
• 해석(Interpretation)과 시각화(Visualization)에 용이
• 데이터를 처리하고 저장하는게 쉽다.

- Singular Value Decomposition (SVD)

• 행렬 U는 docs가 concept과 얼마나 관련이 있는지 의미
• 행렬 람다는 Latent Factor Matrix (각 concept의 강도)
• 행렬 V는 term이 concept과 얼마나 관련이 있는지 의미

- SVD 의 특징

• 분리한 것들을 다시 곱해도(decomposition) 원상 복구가 가능
• 분리해서 나온 3개의 행렬은 유일(unique)하다.
• 행렬 U와 V는 정규 직교(column orthonormal)이다. → Ut*U=I, Vt*V=I
• U와 V의 열 벡터는 직교 유닛 벡터라서 제곱합 계산해보면 모두 1이 나온다.
• 람다는 대각 행렬로, 모든 대각 원소가 고유값(singular value)이며 모두 양수이다. 내림차순으로 정렬되어 있다.

- 예제

• 원래 행렬은 행이 user이고(화살표는 고객의 취향), 열은 movie이다.
• 즉, 각 고객이 영화에 등급을 매긴 데이터 집합을 행렬로 표현한 것
• 분리해서 나온 행렬은 왼쪽부터 순서대로, user-concept 간의 연관성, 고유값 행렬, movie-concept 간의 연관성을 의미한다.

- SVD를 이용한 차원 축소

• 위에서 벡터 v1은 행렬 V(이전의 Right Singular Matrix)의 첫번째 벡터
• 점의 위치를 설명하기 위해 (x,y)라는 두 좌표를 이용하는 것 대신에 하나의 좌표 z를 사용
• 점의 위치는 벡터 v1를 따라 위치
• v1을 선택하는 방법은 오류를 최소화하는 직선을 찾는 것
  • Minimize reconstruction error

• 분산(variance)을 크게 해주는 축이 구별하기 쉬우므로 더 좋음

- 차원 축소를 정확하게 하는 방법

• 가장 작은 고유값을 0으로 만든다.

• 람다의 대각행렬은 얼마나 많이 필요한가? 80-90%

- SVD를 계산하는데 O(nm^2) 또는 O(n^2 m)이 걸린다. 그러나, 고유값만 원하거나 첫 k개의 고유 벡터를 원하거나 matrix is sparse 하면 계산 비용이 적게 들 것

- 차원 축소는 더 작은 개수의 가장 큰 고유 값들을 유지해야 하며, 선형 상관관계를 선택해야 한다. 즉, 전체 행렬의 10% 까지는 원소를 제거해도 되니 빈 셀로 두고 SVD를 계산해도 된다는 의미이다.

데이터 간 유사도

- 모든 데이터는 벡터로 표현 가능

- 일반적으로 내적을 이용해서 데이터간 유사도를 측정

- 내적을 쓰는 이유: 각도를 이용하는데, 예를 들어 0도면 서로 같고 180도면 서로 다르다. 이를 위해 cosin 각도가 활용되므로 내적을 사용하는 것

- 데이터는 많은 것도 문제가 되나 차원(데이터 테이블의 컬럼)이 높은 것도 분석에 문제가 된다. 차원이 높을 수록 내적에 시간이 많이 걸린다.

고차원 데이터 처리하기

- Locality Sensitive Hashing: 비슷한 데이터를 확률적으로 높게 같은 bucket 에 있게하는 방법으로, 기존의 해쉬기법과 달리 비슷한 데이터끼리는 같거나 가까운 bucket 에 둔다는 점에서 차이가 있다.

- Clustering: 비슷한 데이터끼리 군집화 (서로 다른 클러스터는 서로 다른 데이터라고 볼 수 있다.)

- Dimensionality Reduction: 유사도 측정에 관련 없는 데이터를 제거하는 방법

예시: A와 B를 구매한 고객 X 가 있을 때, 고객 Y 가 A를 구매할 경우 B 를 추천하는 경우 여기서 데이터는 고객 X 로부터 수집된 것이다.

필터링의 필요성

- 웹 상에서는 제품에 대해 거의 제로 비용으로 정보를 제공한다.

- 선택지가 많은 것은 사람에게 복잡함을 주기 때문에 추천 시스템으로 필터를 해줄 필요가 있다.

- Long Tail: 주목받지 못하는 아이템이 그래프 상에서 표현된 모양을 일컫는 용어

가로 축은 등수이고, 세로 축은 인기도일 때 실제 상품이 많아 등수 축은 훨씬 긴 범위를 가지는 반면 인기도 축은 훨씬 짧은 범위를 가진다. 따라서, 상품이 많아 주목받지 못하는 아이템이 주목받는 아이템보다 훨씬 많다. 적분 시 위 그림의 노란색 부분이 더 크다.

추천 유형

- Editorial and hand curated: 전문가의 평가로 추천하는 시스템. (ex: 좋아하는 것의 목록, 필수 아이템 목록)

- Simple aggregates: 대중에게 인기 있는 것을 추천. (ex: 탑 10, 가장 인기있는 것, 최근 업로드한 것)

- Tailored to individual users: 각 개인에게 특화된 추천 - Personalized Recommendation - (ex: 아마존, 넷플릭스, … 등)

공식적인 모델

- Utility function: X가 S를 대상으로 매기는 등급, u: X x S → R

• X = set of Customers
• S = set of Items (추천 대상)
• R = set of ratings (예시: 평점)

- R 는 전체적으로 순서있는 집합이다.

유틸리티 행렬(Utility Matrix)

- 일반적으로 sparse matrix (빈칸이 많음) 라서, 연산을 용이하게 하기 위해 빈 셀에 값을 유추해서 저장해놓는다.

핵심 문제

- 행렬에 대해 알려진 등급(ratings)들을 모은다.

• Explicit Feedback: 명확한 유저의 의견을 반영하는 방식 (예시: 평점) → 실제로 잘 동작X
• Implicit Feedback: 암시적인 의견을 반영하는 방식 (예시: 물건 구매/장바구니 행위 자체)

- 알려진 사람(ones)들로부터 모르는 등급(ratings)들을 유추한다. 주로 모르는 등급들에 관심이 많다. 이미 알려져 있는 것에는 흥미가 없다.

- Utility Matrix U is Sparse → 대부분 사람들은 많은 아이템에 평점을 남기지 않는다.

- Cold Start: 어떤 데이터도 없이 시작하는 것 (ex: 새로 개봉한 영화, 새로 가입한 사용자)

- 추천 시스템에 대한 3가지 접근법

• Content-based: 아이템 내용을 기반으로 추천
• Collaborative: 여러 대상을 이용해서 필터링
• Latent factor based: 확실하지 않으나 존재하는 기준이나 카테고리 또는 요소를 이용(잠재 변수 기반)

- 유추하는 방식을 평가 = 추천 방식의 성능과 성공을 평가

컨텐츠 기반 추천 시스템(Content-based Recommendations)

- 주 아이디어: 고객 X에 의해 높게 등급이 매겨진 이전 아이템들과 유사한 아이템을 고객 X에게 추천

• 예시1: 이전 영화에 나온 배우, 디렉터가 출연한 영화 또는 장르가 유사한 영화 추천
• 예시2: 웹사이트, 블로그, 뉴스에서 유사한 컨텐츠를 가진 다른 사이트 추천

- Plan of Action

- 아이템 프로필(Item Profiles): 각 아이템에 대해 프로필을 생성

profile  = set (vector) of features

• 예시1: 영화 - author, title, actor, director, …
• 예시2: 텍스트 - 문서에서 중요한 단어들의 집합

- 예시 2에서 중요한 특징(feature)을 선택하는 방법

• 보통 텍스트마이닝에서는 TF-IDF 를 사용 (단어 빈도 수 / 단어가 나온 문서 빈도 수)
• TF-IDF = Term frequency / Doc Frequency
• Term -> Feature
• Document -> Item

• f : 문서 j에서 단어 i가 사용된 횟수, max f : 문서 j에서 가장 많이 사용된 단어의 사용 횟수
• TFij = f / max f : 문서 j에서 단어 i의 빈도 수
• ni : 단어 i를 사용한 문서의 개수, N : 전체 문서의 개수
• IDFi = log(N/ni) : 단어 i를 사용한 문서의 빈도 수
• Doc Profile = TF-IDF 가 가장 높은 단어들의 집합

- 사용자 프로필(User Profile)

• 등급을 준 아이템 프로필들의 평균에 가중치한 것
• 분산(Variation): 아이템들의 평균 등급의 차이에 의한 가중치

- 예측 귀납(Prediction heuristic): 사용자 프로필 x 와 아이템 프로필 i 가 주어졌을 때, u(x, i) = cos(x, i) 이다. 여기서 cosin 은 방향이 중요함을 의미한다. 얼마나 좋아하는지가 아닌 좋아하는 그 자체(방향성)에 의미를 둔다.

- 장점

1. 다른 사용자에 대한 데이터를 필요로 하지 않는다. (No cold-start or sparsity problems)

2. 독특한 취향을 가진 사용자에게 추천할 수 있다. (일반적이지 못한 사용자들)

3. 새롭거나 인기가 없는 아이템을 추천할 수 있다. (No first-rater problem)

4. 설명을 제공할 수 있다. (추천된 아이템의 내용적인 특징을 리스팅하는 것)

- 단점

1. 유사도에 필요한 특징(feature)을 선택하기 힘들다. (이미지, 영화, 음악 등)

2. 새로운 유저에게 추천하는 것이 힘들다. (사용자 프로필을 만드는 법에서 막힘)

3. 너무 특화된 것들만 추천할 수 있다. (Overspecialization) 예를 들어, 사용자의 컨텐츠 프로필 외의 아이템을 추천하지 않거나, 다양한 흥미를 가진 사람들이 있을 수 있는데 하나만 추천하는 경우가 해당된다. 다른 사용자의 질적 판단을 이용하지 않는다.

협업 필터링(Collaborative Filtering)

[User-user collaborative filtering]

- 사용자를 고려하는 방식으로, 취향이 비슷한 집단에서 누군가 선호한 아이템을 아직 접하지 않았다면 고객에게 그 아이템을 추천

- N = 고객 x의 등급 부여 방식(ratings)과 유사한 방식(ratings)을 가진 다른 사용자의 집합

- 집단 N 에서 사용자들의 등급 부여 방식을 기반으로, 고객 x가 매긴 등급을 측정(유추)

- 유사한 사용자를 찾는 법 (데이터간 유사도 측정 방식)

• rx = 고객 x의 아이템별 등급(ratings)을 원소로 갖는 벡터

• 자카르드 유사도 측정법(Jaccard similarity measure): 교집합 크기 / 합집합 크기
  • 문제: 특정 등급을 무시할 수 있다.

• 코사인 유사도 측정법(Cosine similarity measure): cos(rx, ry) = rx*ry / (|rx|*|ry|)
  • 두 유저의 rating vector 를 내적한 결과를 벡터의 길이의 곱들로 나눔. 단, 여기서 평가되지 않은 경우는 0점을 주어 계산
  • 문제: 누락된 등급을 음수로 표현할 수 있다.

• 피어슨 상관 계수 (Pearson correlation coefficient)
  • Sxy = 고객 x와 y 모두에 의해 등급이 매겨진 아이템들 (추가 이론은 위키피디아 참고)

- 유사도 측정 항목(Similarity Metric)

• 직관적으로 봤을 때 원하는 것: sim(A,B) > sim(A,C)
• 자카르드 유사도: ⅕ < ½ 
  • A와 B의 합집합 크기(총 컬럼 개수 5개, HP1, HP2, HP3, TW, SW1)는 5, 교집합 크기는 1
  • A와 C의 합집합 크기(총 컬럼 개수 4개, HP1, TW, SW1, SW2)는 4, 교집합 크기는 2
• 코사인 유사도: 0.386 > 0.322 → 빈 칸(0)을 처리하지 못해서 A와 C의 반대 성향을 잡지못함
• 해결책: 빈 등급을 음수값으로 맞춰놓고, 행의 평균을 빼고 코사인 유사도를 측정하면 피어슨 상관 계수와 동일한 결과를 낸다.
  • 0.092 > -0.559

A행의 평균은 10/3 이다.

- 등급 예측(Rating Predictions) → 유사도 측정 항목을 어떻게 활용하는가?

• rx = 고객 x의 등급들의 벡터
• N = 아이템 i를 등급매겼던 고객 x와 대부분 유사한 k명의 고객들의 집합
• rxi = 고객 x가 아이템 i에 매긴 등급 = 특정 집단(N)이 아이템 i에 준 점수들의 평균

[Item-Item collaborative filtering]

- 아이템은 고객(user)들의 등급으로 표현된다. 벡터의 각 원소가 각 유저가 매긴 등급(rating)

- 알고리즘

1. 아이템 i와 유사한 다른 아이템들을 찾는다.

2. 유사한 아이템에 대한 등급을 기반으로 아이템 i에 대한 등급을 평가한다.

3. 동일한 유사도 측정 항목과 user-user 모델에서와 같이 예측 함수를 사용할 수 있다.

- rxj = 고객 x가 평가한 아이템 j의 등급

- Sij = 아이템 i와 j의 유사도

- N(i;x) = 아이템 i와 유사한 고객 x에 의해 평가된 아이템들의 집합 (음수인 유사도는 제외)

위의 식으로 아이템 i의 등급을 예측 (다른 고객의 정보가 필요없음)

고객 5가 등급을 매긴 영화들 중 1번 영화와 유사한 영화들을 탐색한 다음,

등급이 없는 영화에 대해 점수를 몇 점 줄 것인지 예측, 왼쪽 sim(1, m)는 1번 영화와 m번째 영화와의 유사도

- CF: Common Practice

• 아이템 i와 j의 유사도 Sij 를 정의
• k개의 가장 가까운 이웃 선택
• N(i; x) = 고객 x에 의해 등급이 매겨진 아이템 i와 가장 유사한 아이템들
• 가중치된 평균으로 등급 rxi를 측정

• b: bias로, 유저별 개인차 또는 아이템별 개인차를 의미한다.
• u: 전체 등급의 평균

[비교 분석: Item-Item vs User-User]

- 실제로, item-item이 user-user보다 협업 필터링이 더 잘 동작하는 것으로 관찰되어왔다.

- 그 이유는 사용자가 아이템보다 개인차가 더 크기 때문이다.

[협업 필터링 장단점]

- 장점: 어떤 종류의 아이템이든지 잘 동작한다. 특징을 선택할 필요가 없다. (No feature selection, only rating vector)

- 단점:

1. Cold Start: 시스템에서 맞출만한 충분한 고객들이 필요하다.

2. Sparsity: 사용자 또는 등급 행렬 (user/ratings matrix)는 대부분 비어있다. 동일한 아이템을 등급을 매긴 고객을 찾기가 힘들다.

3. First rater: 이전에 등급이 매겨지지 않은 아이템을 추천할 수 없다. (새로운 아이템이나 독특한 아이템들)

4. Popularity bias: 인기 있는 아이템만 추천하는 경향이 있다. 독특한 취향을 가진 누군가에게 추천할 수 없다.

- 하이브리드 방법: 둘 이상의 다른 추천을 구현하거나 예측을 결합하는 방법으로, 보통 선형 모델을 사용한다.

예시: 컨텐츠 기반에 협업 필터링을 추가한 방법: 새로운 고객이나 아이템에 대해서(cold start) 프로필을 활용하고 그 외는 협업 필터링을 이용하는 방식 

Remarks & Practical Tips

- 평가(Evaluation): 알려진 등급들을 가지고 예측한 것을 비교한다. (Dataset, Testset 분리)

Root-mean-square error (RMSE)

Precision at top 10 - 퍼센트로 상위 10개만 뽑기

Rank Correlation - 랭크의 유사도 (시스템과 고객의 완전한 랭킹 사이의 스피어맨 상관 관계)

- 또 다른 접근법: 0/1 모델

• Coverage: 얼마나 추천가능한가, 예측할 수 있는 시스템에서 아이템과 사용자의 수
• Precision: 예측의 정확도
• Receiver operating characteristic (ROC): false positive 와 false negative 사이의 Tradeoff 곡선 → 의학영역에서 많이 사용

- 오류 측정 항목(Error metrics)

• 문제: 정확도에 대한 초점이 강할수록 요점을 놓칠 때가 있다.
  • Prediction Diversity: 예측 다양성
  • Prediction Context: 예측 상황
  • Order of predictions: 예측 순서

- 실제로, 높은 등급을 예측하기 위해 주의해야만 한다. RMSE 는 높은 등급에 대해서는 잘 동작하나 아닌 것들에 대해서는 안좋게 동작하는 방법에 불리할 수 있다.

- 복잡도/속도(Complexity/Speed): k명의 가장 유사한 고객들을 찾는 것은 비용이 비싸다. 런타임 상에 수행하기에는 미리 계산해야 함.

- 해결책: 고차원에서 가장 가까운 이웃을 탐색하는 방법 (LSH), 클러스터링, 차원 축소

- 팁

• 변덕스러운 알고리즘이 잘 동작하려는 노력때문에 데이터 크기를 줄이려고는 하지 말 것
• 큰 데이터에 대해서는 단순한 방법이 최고다.
• 데이터를 더 추가하는 것 → 더 많은 데이터가 더 나은 알고리즘을 이기기도 한다. (추천 성능 측면에서만)

잠재 요인 모델(Latent Factor Models)

- Latent Factor: 중요한데 존재하지 않는 카테고리(잠재 변수)

• 예시: 넷플릭스 - 100 만개의 등급(ratings), 2000 ~ 2005 년간의 데이터, 평가 기준 = RMSE

- 로컬 & 전역 효과 모델링 (Modeling local & global effects)

• 전역 효과 예시: 평균 영화 등급이 3.7이고, 식스센스의 평점이 평균 보다 0.5 점 높을 때, Joe는 평균 보다 0.2점을 더 낮게 평가한다면, 식스센스는 4점(=3.7+0.5-0.2)일 것이다. 
• 로컬 효과 예시: local neighborhood (CF/NN) 에서는 Joe 는 영화 Signs 과 비슷한 걸 좋아하지 않는다. → 최종적으로 Joe 는 평점을 3.8점 줄 것이다. (두 영화가 유사하기 때문에 이전의 안좋은 평가를 반영하여 다음 영화의 점수를 예측)

- 협업 필터링(CF): 나온지 꽤 되었고 가장 인기있는 협업 필터링 방법

1. Item-Item 방법으로, 유사한 영화들의 등급으로부터 모르는 등급을 도출

2. 아이템 i와 j의 유사도 Sij 를 정의

3. k개의 가장 가까운 이웃을 선택, 그리고 등급을 계산

• N(i; x) = 고객 x에 의해 등급이 매겨졌던 아이템 i와 가장 유사한 아이템 집합
• rxj = 아이템 j에 대해 고객 x가 매긴 등급

그러나 실제로 bias 를 추가하여 아래와 같이 계산

Problems/Issues 2번은 고객 간의 공통성을 놓치고 있다는 의미

해결책은 RMSE 를 최대한 낮춰주는 경우의 가중치 Wij가 가장 좋다.

- Interpolation Weight Wij

• 가중치된 평균보다 가중치된 합을 사용 (아이템 i와 그것의 이웃 j 사이의 관계)

• 표기법
  • N(i; x) = 영화 i와 유사한 고객 x에 의해 등급이 매겨진 영화들의 집합
  • Wij = interpolation weight
  • 가중치 모델은 고객 x에 의존적이지 않으며, 영화 쌍(pairs) 사이에서 상호작용하는 것
  • 오류 측정 항목: 학습 데이터에서 SSE를 최소화하는 가중치 찾기

• 가중치 설정
  • Wij 는 영화 i를 평가했던 모든 다른 고객과 고객 x를 기반으로 학습되거나 측정된다.

- 최적화를 통한 추천

• 목표는 좋은 추천 기능을 하는 것 → RMSE 사용 → 낮을 수록 더 나은 추천
• 고객이 보지 못한 아이템에 대해 추천을 하는 것 → 실제로는 어려움
• 알려진 등급(user, item)에 대해 잘 작동하도록 시스템을 구축하는 것 → 모르는 등급을 잘 예측할 수 있다.
  • 목표 함수(objective function) 정의 → 최적화 문제를 해결
  • 학습 데이터에서 SSE를 최소화하는 가중치 찾기, 가중치를 벡터로 생각하자

• 함수 최소화하는 단순한 방법
  • 어떤 점 y 에서 시작 → 미분 계산
  • 그래프에서 움직이는 방향은 미분의 반대 방향

    

  • 미분 값이 0인, 최저점 도달(converged)할 때까지 반복
  • 기울기가 작을 수록 움직이는 간격이 작아야 한다. 안그러면 값이 그래프를 벗어날 수 있음

object function 을 가중치 Wij 로 미분해서 미분값이 0이 되는 가중치를 탐색

그러나 실제 w를 찾기는 어려우므로 이전 W와의 차이가 0인 새로운 W를 탐색

- 가중치는 유사도를 사용하지 않음. 둘은 다르다. 유사도는 명시적으로 이웃 아이템들 사이에 내부 관계에 대해 설명하는 것

- Latent Factor Models → Singular Value Decomposition

• SVD: 다시 곱해도 원래대로 (노란 부분을 원복) 잘 나오도록 벡터를 분해하는 것
• 가정: 노란 부분을 잘 원복하면 흰색도 원복이 된다.
• factor는 많을수록 정확하게 맞출 수 있으나, overfitting 이 발생할 수 있다. 이는 예측 실패율을 높인다.
• 위의 경우 등급 행렬(rating matrix R)을 Q*Pt 의 곱으로 근사할 수 있다.
• Factor들의 곱으로 등급매기기(Ratings)
  • 아이템 i에 대해 고객 x의 등급이 없으면 어떻게 측정하는가?

Q의 2번째 행과 Pt의 5번째 열을 내적

엔트리가 없을 때는 SVD는 정의되지 않는다. 행렬 P, Q를 찾기 위한 구체적인 방법을 사용해야 한다.

(그냥 SVD는 동작X) → 엔트리가 있는 값들(not missing data)만 가지고 오류의 최솟값을 찾는다.