Move Fast

테스트 환경: ubuntu 16.04

문제는 Rust 바이너리를 리버싱해서 플래그를 찾으라는 거다. 2개의 파일 rs, result 이 주어지고 각 파일의 실행결과는 다음과 같다.

flag 라는 파일이 없어서 난 오류로 파일을 별도로 만들면 헥사값이 출력된다.

아래는 result 파일 내용이다.

파일명이 result 인 걸로 보아 rs의 결과가 위와 같이 나오도록 하는 플래그 값을 찾으라는 의도임을 알 수 있다.

flag 의 내용을 모르므로 직접 리버싱해서 알고리즘을 찾아야 한다. 근데 이 바이너리는 쓸데없이 함수 호출이 많아서 디스어셈블 했을 때 굉장히 난감했다. 결국 gdb로 직접 디버깅해보기로 했다.

디버깅의 목적은 파일 내용을 읽어서 어떤 알고리즘을 수행하는지 알아내는 것이다. 그러려면 다음과 같은 2가지 정보를 알아야 한다.

1. 파일 내용이 저장되는 메모리의 위치

2. 위에서 찾은 위치에서 어떤 변화를 일으키는 (알고리즘을 수행하는) 명령어의 주소

위의 정보를 얻기 위해 먼저 read, write 함수에 bp를 걸고 malloc/free를 체크했다.

힙 메모리를 관찰한 이유는 실제로 파일 내용이 스택에 저장되기 보다는 힙에 저장될 가능성이 높다고 확신했기 때문이다.

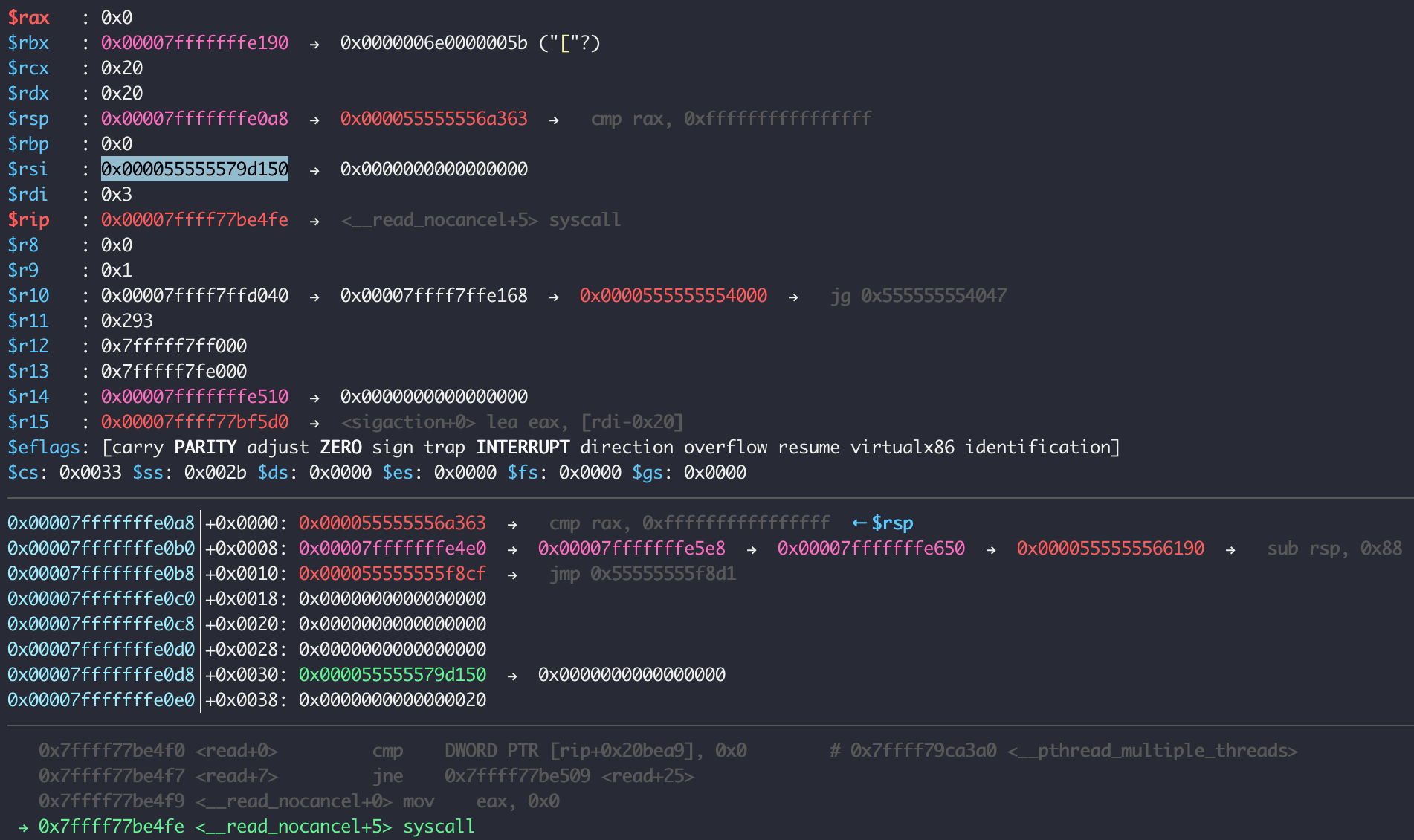
맨 처음에 호출되는 read에서 2번째 인자인 rsi 에 힙 주소가 저장된 것을 알 수 있고, 실행 후 파일 내용이 힙에 저장되는 걸 볼 수 있다.

아래는 초기 힙 영역의 모습이다.

아직까지는 파일 내용만 입력받았기 때문에 별다른 내용이 보이진 않는다. 바로 write() 으로 넘어가보자.

맨 처음에 살펴본 rs 바이너리의 실행 결과가 힙에 저장되었고 그 내용을 출력하는 걸 볼 수 있다.

힙의 상태는 다음과 같다.

0x55555579d290 위치는 출력 내용이 저장된 것을 알 수 있고, 처음에 파일 내용 ("A"*8)을 저장한 곳에는 다른 값이 들어가 있다. 그리고 그 사이를 살펴보면 출력 내용에 해당하는 헥사값(빨간 박스)이 저장된 것이 보인다. 따로 떨어져 있는 건 아마 복사하는 과정이 있어서 그런 듯하다.

여기까지 정리해보면, 0x55555579d150 에는 원래 파일 내용이 저장되어 있었고, 0x55555579d230과 0x55555579d260 에는 알고리즘의 수행 결과가 저장되어 있다. 처음에 필요한 정보인 메모리의 위치를 알아냈으니, 해당 위치를 이용해서 알고리즘을 수행하는 함수를 찾아야 한다.

코드가 복잡하고 호출되는 함수가 많기 때문에 다짜고짜 함수를 찾아가는 것보다 조금 이분법(?)적인 방법을 선택하기로 했다.

read() 를 호출했을 때의 trace 내용은 위와 같다. (최대 10개만 나열해서 보여주므로 자세히 보고 싶으면 bt 명령어를 써야한다.)

아무튼 trace 했을 때 따라 들어온 명령어의 다음 명령어들에 각각 bp를 걸고 실행할 때마다 힙의 변화를 살펴보면, 알고리즘을 수행하는 명령어를 찾을 수 있다.

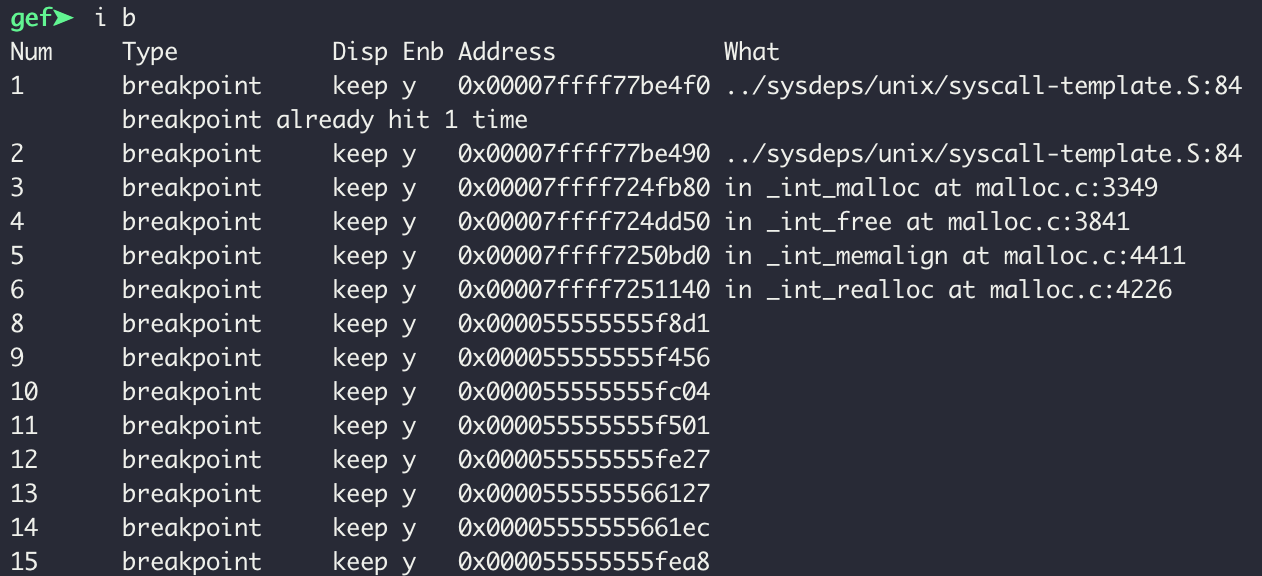
계속 실행해보면 14 번째 bp가 걸린 0x5555555661ec 명령어를 실행하고 나면 힙이 바뀐다. 즉, 그 다음 bp 가 걸린 명령어 (0x5555555661ea8) 이전에 알고리즘이 수행된다는 것이다. 

0x5555555661ec 에서의 코드를 살펴보면 call 명령어가 많은데 싹다 bp를 걸어서 이전에 했던 행동을 똑같이 반복한다.

여기서는 운이 좋게도 맨 처음 함수 호출 이후에 바로 힙의 변화가 일어난다.

눈여겨 보고 있던 0x55555579d230 위치에 헥사값이 들어갔다. 즉, 0x55555555dc90 에서 알고리즘을 수행한다는 것을 알 수 있다.

아무튼 이런 방식(call 에 bp걸고 입력값 관찰)으로 계속 진행해보면 알고리즘을 수행하는 특정 코드 영역을 찾게 된다.

call 0x55555555dc90

---> call 0x555555566ce0

------> call 0x55555555b840

... 생략

---------------------------> call 0x55555555de70

------------------------------> call 0x55555555d7f0

---------------------------------> call 0x555555559570 : 0x55555579d230 위치에 파일 내용을 복사

---------------------------------> call 0x55555555eab0 : 파일 내용을 1바이트씩 변경

최종적으로 함수 0x55555555d7f0 을 호출해서 입력값을 1바이트씩 변경하는데 호출당시 인자를 살펴보면 입력값 외 다른 값이 별도로 들어간다. (입력값의 메모리 위치가 처음(0x~150 --> 0x~180)과 다른 것은 중간에 입력값을 복사해서 생긴 것이다. - 별로 중요하진 않음..)

함수 안으로 들어가보면 1바이트씩 변경하는 함수의 인자를 살펴볼 수 있는데 익숙한 값이 보인다.

계속 실행해보면 알겠지만 0x55555579d1c0 위치가 아니라 0x55555579d1c1 부터 1바이트씩 가져와 사용자 입력값 1바이트와 연산을 수행한다.

구체적인 연산 과정은 직접 디버깅해볼 수 있겠지만 1바이트씩 변경하는 부분은 그냥 디컴파일해서 봤다. ida 나 ghidra에서는 함수 이름이 코드 간 오프셋이기 때문에 저 위치와 코드 베이스 주소간 오프셋(0x55555555eab0 함수는 0xaab0 오프셋이다.)을 검색해보면 함수를 찾을 수 있다.

// 0x55555555eab0
short oneByteEncode(char seedByte, char userByte) {
	short ret, sVar, uVar;
	ret = 0;
	sVar = seedByte;
	uVar = userByte;

	while (uVar) {
		if ((uVar & 1) == 1) ret ^= sVar; // XOR
		uVar = (short) uVar >> 1; // 2로 나눔
		sVar *= 2; // 2배 곱함
		if (sVar >= 0x100) sVar ^= 0x11d; // XOR
	}
	return ret;
}

(다행히 알아보기 쉬운 코드였다.)

계속해서 디버깅을 해보면 다음과 같은 과정으로 알고리즘이 수행되는 것을 알 수 있다.

1. 사용자의 입력을 16바이트 복사한다.

2. 첫번째 바이트와 Seed 문자열(0x55555579d1c1)의 각 바이트(=j번째 바이트)를 인자로 oneByteEncode 함수를 호출한다.

3. oneByteEncode 함수의 반환값은 각각 복사된 입력값의 각 바이트(=입력값에서 j번째 떨어진 바이트)와 XOR 연산이 되어 값을 바꾼다.

* 여기서 oneByteEncode 는 Seed 문자열의 길이(32바이트)만큼 수행되므로, 입력값을 16바이트 복사하더라도 16바이트 이후에는 0x00 과 oneByteEncode 의 결과를 XOR 하게 된다.

4. 두번째 바이트로 2,3 과정을 반복한다. (이 때 복사된 위치는 3번 과정으로 바뀐 값이 저장되어 있다.)

5. 16번째 바이트까지 2~3을 계속해서 반복한다. (다 수행하고 나면 48바이트가 나온다.)

6. 다수행하고 나면 48바이트가 나오고 여기서 첫 16바이트는 버린다.

7. 사용자의 입력 중 다음 16바이트 복사해서 1번부터 수행한다. 각 결과물은 이전 결과물 뒤에 추가한다.

// 0x55555555d7f0
char* sub_97f0(char *userInput, char *seedStr) {
   char *ret = 0;

   for (int k=0; userInput[k] != 0; k+=16) {
      char tmp[48];
      char result[32];
      memset(tmp,0,sizeof(tmp));
      memcpy(tmp,&userInput[k],16); // 16바이트 단위로 복사

      for (int i=0; i<16; i++) {
         for (int j=0; j<32; j++) {
            tmp[i+j+1] ^= oneByteEncode(seedStr[j], tmp[i]);
         }
      }

      memcpy(result, &tmp[16], 32); // 첫 16바이트는 버린다.
      concat(ret,result);
   }
   return ret;
}

(디버깅해서 살펴본거기 때문에 디컴파일 했을 때의 결과랑 내용이 다를 수 있다.)

이제 알고리즘을 알아냈으니 반대로 디코딩하는 알고리즘을 짜야한다. (여기서 생각보다 시간이 많이 걸렸다.)

result 에서 보인 헥사값은 128바이트인데, 사용자의 입력값 16바이트당 32바이트의 문자열을 얻기 때문에 128/32 = 4 번 복사가 이루어졌음을 알 수 있다. 즉 우리는 49 ~ 64바이트의 입력값을 넣으면 된다.

디코딩은 인코딩하는 과정을 뒤집으면 된다.

Seed = [
    0x74, 0x40, 0x34, 0xae, 0x36, 0x7e, 0x10, 0xc2,
    0xa2, 0x21, 0x21, 0x9d, 0xb0, 0xc5, 0xe1, 0x0c,
    0x3b, 0x37, 0xfd, 0xe4, 0x94, 0x2f, 0xb3, 0xb9,
    0x18, 0x8a, 0xfd, 0x14, 0x8e, 0x37, 0xac, 0x58
]
    
def findHex(idx, target):
    for i in range(256):
        result = oneByteEncode(Seed[idx],i)
        if result == target:
            return i
    assert (1 == 0)

def decode(data):
    assert len(data) == 32
    data = [ 0 for i in range(16) ] + data
    for i in range(15,-1,-1):
        data[i+32] = data[i+32] ^ 0x00
        data[i] = findHex(31, target=data[i+32])
        for j in range(30,-1,-1):
            data[i+j+1] ^= oneByteEncode(Seed[j],data[i])

    return data[:16]

디코딩의 정당성 증명은 다음과 같다.

예제) ABCDEFGH
출력) 91 21 70 be 6c 27 f6 aa ff 00 a2 47 a4 f6 db 24 10 43 6b a2 46 a5 ef 09 08 c8 ff b2 8d b8 58 a3

23 d7 6d ea 5a d8 7a 41   1a 6a 4c 0f 00 07 c4 23
d1 4b bf ea d4 c2 ef ed   9c e9 cb ff d9 df 7d 2d
98 9a 54 12 e2 5c df 34   00 06 24 80 67 c8 ad 65

// 마지막 연산 이후 메모리
23 d7 6d ea 5a d8 7a 41   1a 6a 4c 0f 00 07 c4 23
aa f6 27 6c be 70 21 91   24 db f6 a4 47 a2 00 ff
09 ef a5 46 a2 6b 43 10   a3 58 b8 8d b2 ff c8 08

1. 32바이트 문자열의 맨 마지막 바이트는 항상 0x00과 XOR 연산이 이루어진다.

위의 경우 마지막 바이트 0xa3 이전에는 0x00 이었다. 즉, 0x00 ^ encode(...) = 0xa3 이므로,

마지막 oneByteEncode(...) = 0xa3 ^ 0x00 = 0xa3 임을 알 수 있다.

2. 들어가는 인자는 oneByteEncode(Seed[31], B[15]) 이므로, 아스키코드 범위(0~255)의 브루트포싱으로 B[15]를 구할 수 있다.
실제로 역연산을 해보면 0x1a 가 정상적으로 나온다.

3. 초기값인 B[15] (구체적으로 말하자면 가장 마지막에 구해지는 B[15]이다.)를 구할 수 있으므로,
점화식에서 연쇄적으로 이전의 B[16] ~ B[46] 까지의 값을 구할 수 있게 된다.

* 마지막 B[16]~B[47] 연산 과정에서 사용된 B[15]는 최종값이므로 2번에서 구한 걸 계속 사용하면 된다.

4. 좀 더 설명하자면, 이전의 B[46]을 구할 수 있기 때문에 구한 B[46] 으로 1번 과정처럼 (마지막으로 구한) B[14]를 구할 수 있게 된다.

증명)

별도의 debug() 함수를 만들어서 관찰해보면 정상적으로 스크립트가 실행된다.

전체 코드

#!/usr/bin/python

##### script.py

Seed = [
    0x74, 0x40, 0x34, 0xae, 0x36, 0x7e, 0x10, 0xc2,
    0xa2, 0x21, 0x21, 0x9d, 0xb0, 0xc5, 0xe1, 0x0c,
    0x3b, 0x37, 0xfd, 0xe4, 0x94, 0x2f, 0xb3, 0xb9,
    0x18, 0x8a, 0xfd, 0x14, 0x8e, 0x37, 0xac, 0x58
]

def oneByteEncode(seedByte, userByte):
    ret = 0
    sVar = seedByte
    uVar = userByte
    while uVar > 0:
        if (uVar & 1) == 1:
            ret ^= sVar # XOR
        uVar = uVar >> 1 # divide by 2
        sVar *= 2
        if sVar >= 0x100:
            sVar ^= 0x11d # XOR
    return ret


def tostr(arr):
    s = ""
    for el in arr:
        s += "%02x " % el
    return s


def debug(arr):
    for i in range(0, 64, 16):
        left = list(arr[i:i+8])
        left.reverse()
        right = list(arr[i+8:i+16])
        right.reverse()
        print tostr(left) + "  " + tostr(right)

def encode(userInput):
    maxSize = 64
    data = [0 for i in range(maxSize)]
    for i in range(len(userInput)):
        data[i] = ord(userInput[i])

    idx = 0
    result = []
    while idx < maxSize:
        if data[idx] == 0: break
        tmp = [ data[idx+i] for i in range(16) ]
        tmp += [ 0 for i in range(32) ]
        debug(tmp)
        for i in range(16):
            for j in range(32):
                tmp[i+j+1] ^= oneByteEncode(Seed[j], tmp[i])
            debug(tmp)

        result.append(tostr(tmp[16:]))
        idx += 16

    return ' '.join(result)

def findHex(idx, target):
    for i in range(256):
        result = oneByteEncode(Seed[idx],i)
        if result == target:
            return i
    assert (1 == 0)

def decode(data):
    assert len(data) == 32
    data = [ 0 for i in range(16) ] + data
    for i in range(15,-1,-1):
        debug(data)
        data[i+32] = data[i+32] ^ 0x00
        data[i] = findHex(31, target=data[i+32])
        for j in range(30,-1,-1):
            data[i+j+1] ^= oneByteEncode(Seed[j],data[i])
        debug(data)

    return data[:16]

def main(userInput):

    data = [ int(_byte, 16) for _byte in userInput.split(' ') ]
    ret = ''
    for i in range(0,len(data),32):
        result = decode(data[i:i+32])
        for ch in result:
            if ch > 0:
                ret += chr(ch)
    return ret

if __name__ == '__main__':
    s = raw_input("User Input: ")
    print main(s)

이분 매칭 문제

- 완벽한 매칭 그리고 제약된 집합

• 우리는 완벽한 매칭으로 이러한 과제를 언급한다. 이분 그래프의 양쪽의 노드들의 개수를 동일하게 할 때, 완벽한 매칭은 왼쪽과 오른쪽에서의 노드들을 할당하는 것이다.
  • 각 노드는 할당되어진 노드로 엣지에 의해 연결되어진다.
  • 왼쪽의 어떤 다른 두 노드는 오른쪽에서 같은 노드로 연결되지 않는다. (1:1)
• 제약 집합(Constricted Sets)
  • 이분 그래프가 완벽히 매칭이 된다면, 완벽한 매칭을 형성하는 엣지를 표시하는 것을 설명하기 쉽다. 그러나 만약 이분 그래프가 완벽한 매칭을 갖지 않는다면? 완벽한 매칭이 없다는 것을 누군가에게 납득시킬 수 있는가?

- 제약 집합과 매칭 이론

• 제약 집합: S를 노드의 집합이라고 하고, N(S)를 이웃 노드의 집합이라고 할 때, S가 N(S)보다 엄격하게 더 크다면, S는 제한되어야 한다.
• 매칭 이론: 만약 이분 그래프(노드의 개수는 왼쪽,오른쪽 동일)가 완벽한 매칭을 갖지 않는다면, 제약 집합을 포함해야만 한다. 즉, 제약집합이 있으면 완벽한 매칭은 존재하지 않는다.

그림 (b)에 대한 설명: Valuations 에서 가장 큰 값을 갖는 경우의 Room 으로 매칭이 이루어진다. 근데 7,6 처럼 차이가 크지 않은 경우(두번째 집합)는 다음 값을 보고 행동을 결정한다. 5,2의 차이는 7,6보다 차이가 크기 때문에 Room 2 와 Room3 의 엣지를 크로스 매칭한다.

- 최적화 할당

• 노드가 얻는 각각의 valuation의 총합을 크게 만드는 것
• 반드시 모든 노드에게 좋아하는(가치가 높은) 아이템(노드)을 할당할 필요는 없다.

- 가격 & 마켓-정리 속성(Market-Clearing Property)

• 중앙 조정(Central coordination): 최적화 할당 혹은 완벽한 매칭을 결정하는 중앙 관리자
• 마켓을 분권화한다.
  • 아이템에 가격을 매기는 특정 틀(scheme)로 중앙 관리자를 대체한다.
  • 개개의 노드가 valuations 와 가격에 따라 self-interest를 따르게 한다.

- 가격, 페이오프(payoffs), 그리고 선호되는 판매자

• 가격과 payoffs: 각 판매자 i가 집을 가격 Pi로 판매한다고 할 때, 만약 구매자 j가 해당 가격에 집을 구매한다면 구매자의 payoff는 그 집에 대한 valuation에서 지불해야 했던 금액을 뺀 것으로 정의된다. (Vij - Pi) 가격 집합이 주어졌을 때, 구매자 j가 payoff를 최대화하길 원한다면, 판매자 i로부터 이 품질 Vij - Pi를 최대화하도록 구매할 것이다.
• 다음은 경고사항이다.
  • 첫째, 이 품질이 몇몇 판매자 간의 동점에서 최대화되어진다면, 그 때 구매자는 그들 중 하나를 고름으로써 payoff를 최대화할 수 있다.
  • 둘째, 만약 payoff Vij - Pi가 판매자의 모든 선택에 대해 음수라면, 그 때 구매자는 어떤 것도 구매하지 않을 것이다. 여기서 구매자가 단순히 아무것도 하지 않음으로써 payoff=0을 얻을 수 있다.
• 구매자 j의 선호되는 판매자들
  • 구매자 j의 payoff를 최대화시키는 판매자, payoff >= 0

- 선호되는 판매자 그래프 & Market-Clearing Prices (MCP)

• 선호되는 판매자 그래프: 각 구매자와 선호되는 판매자 혹은 판매자들 사이에 엣지를 연결
• Market-Clearing Prices(MCP)
  • 가격 집합은 선호되는 판매자 그래프가 완벽한 매칭을 가지는 경우 market-clearing이다.
  • 구매자들이 다른 아이템을 얻음으로써 구매자들 사이에서 언쟁이 해결된다.

- Properties of MCP

• MCP의 존재: 구매자 valuations의 집합에 대해, market-clearing prices의 집합이 존재한다.
• MCP의 최적성(Optimality)
  • market-clearing prices의 어떤 집합에 대해, 선호되는 판매자 그래프에서의 완벽한 매칭은 판매자들의 구매자로의 할당될 때 valuation의 총합을 최대가 되게 한다.
  • market-clearing prices의 집합과 선호되는 판매자 그래프에서의 완벽한 매칭은 모든 판매자들과 구매자들의 payoff의 가능한 합을 최대화한다.
• MCP의 최적성 보이기 
  • 선호되는 판매자 그래프에서의 완벽한 매칭을 M이라 할 때, M의 총 payoff는 각 구매자가 자신의 payoff를 최대화하는 물건을 잡고 있으므로, M은 최대 총 payoff를 가진다. Total payoff of M = Total Valuation of M - Sum of all prices로 정의된다. → max total payoff means max total valuation

- MCP 구성하기 

• 구매자 valuations의 임의의 집합이 주어졌을 때, MCP로 가는 절차가 있다. 실제로 그 절차는 auction(경매)의 한 종류이다. 다수의 경매되는 물품들과 다른 valuations를 가지는 다수의 구매자들이 있다.
• 경매가 이루어지는 방식
  • 초기에 모든 판매자들은 가격을 0으로 한다.
  • 구매자들은 선호되는 판매자를 고른다.
  • 그리고 선호되는 판매자 그래프를 확인한다. 만약 이 그래프가 완벽한 매칭을 갖지 않는다면, 구매자들의 제약 집합 S가 존재한다. 이웃 노드의 집합 N(S)은 판매자들의 집합임을 고려하라. 집합 S에 있는 구매자들은 오로지 N(S)에 있는 판매자들이 판매하는 것을 원한다. 그러나 S에 있는 구매자들보다 N(S)에 있는 판매자들이 더 적다. 그래서 N(S)에 있는 판매자들은 높은 수요(high demand)를 갖는다. 너무 많은 구매자들이 그들에게 관심을 보인다.
  • 구매자들은 판매자가 한 단위씩 가격을 올릴 때마다 반응하고 경매는 그 때 계속된다.
• 다른 방법도 있는데, 가격에서 reduction 연산은 하는 것이다. 가장 작은 가격이 0이 되도록 가격을 스케일하는데 유용하다. 그러므로 모든 가격이 엄격히 0보다 큰 노드에 도달한다면, 각각의 가격으로부터 p를 빼서 가격을 낮춘다. 이는 가장 낮은 금액을 0으로 만들고 동일한 상대량에 의해 모든 다른 가격들도 바뀐다.

- MCP 구성을 위한 경매 절차

1. 각 라운드에서 시작, 가장 작은 가격이 0인 현재 가격 집합이 있다.

2. 선호되는 판매자 그래프를 구성하고 완벽한 매칭이 있는지 검사한다.

3. 완벽한 매칭이 있으면, 현재 가격들이 market-clearing 상태이다.

4. 완벽한 매칭이 없다면, 구매자 제약 집합 S와 이웃 노드의 집합인 N(S)를 찾는다.

5. N(S)에 있는 각 판매자는 (동시에) 한 단위씩 가격을 올린다.

6. 필요하다면, 가장 작은 가격이 0이 되도록 가격을 낮추는데 다른 가격들로부터 동일한 상대량을 각각 빼준다.

7. 새로운 가격 집합으로 경매의 다음 라운드를 진행한다.

처음에 0으로 시작해서 1개의 노드만 N(S)에 있다. 그 노드의 가격을 올리고 다시 경매를 시작한다.

계속 가격을 올리다 보면 N(S)에 판매자 노드가 하나씩 추가된다. 추가되면서 다음 라운드 직전에 N(S)에 있는 모든 판매자 노드는 동시에 한 단위씩 가격을 올린다. 위 그림에서 (d)는 가격 집합이 market-clearing prices 상태이다.

• 경매는 끝이 나야만 한다.
  • 사실, 가격이 멈추지 않고 영원히 바뀔 수는 없다. 경매는 항상 끝나야 한다. 이것을 보여주는 방법은 어떤 종류의 잠재적 에너지가 그것이 실행될 때 경매에서 고갈되고 있다는 정확한 감각을 알아내는 것이다. 경매는 이 잠재적인 에너지를 초기에 한정된 공급으로만 시작하므로, 결국 고갈되어야 한다.
  • 여기 우리가 이 잠재적 에너지 개념을 정확히 정의하는 방법이 있다. 현재 가격 세트의 경우, 구매자가 현재 판매자로부터 받을 수 있는 최대 지급액이 될 가능성을 정의하십시오. 이것은 구매자의 잠재적 보상이다. 만약 현재의 가격이 market-clearing prices 이라면 구매자는 실제로 이 보상을 받을 것이다. 우리는 또한 판매자의 잠재력이 그가 청구하는 현재 가격이라고 정의한다. 이것은 판매자의 잠재적 보상이다. 현재 가격이 market-clearing prices 이라면 판매자는 실제로 이 보상을 받을 것이다. 마지막으로, 우리는 경매의 잠재적 에너지를 구매자와 판매자 모두 모든 참가자의 잠재력의 합으로 정의한다.
  • 퍼텐셜 payoff는 현재 가격 정책에서 책정 가능한 최대 payoff